
分析 根据方程根的个数与判别式之间的关系证明△>0恒成立,由题意判断出另一个根的范围,再由f(1)>0求出a的范围,利用f(0)<0进一步确定两个根的关系,再由韦达定理求出a范围,再取交集.
解答 解:∵|x2|<x1(1-x2),∴x1(1-x2)>0,
又∵0<x1<1,∴x2<1
设f(x)=(a2+1)x2-2ax-3,∵方程有两根,∴△=4a2+12(a2+1)>0恒成立,
则f(1)=a2-2a-2>0,解得a>1+$\sqrt{3}$或a<1-$\sqrt{3}$;
∵f(0)=-3,
∴x2<0<x1<1,
则|x2|<x1(1-x2)可化简为:x1+x2>x1x2,
利用韦达定理得$\frac{2a}{{a}^{2}+1}$>-$\frac{3}{{a}^{2}+1}$,
解得a>-$\frac{3}{2}$.
∴实数a的取值范围是:(-$\frac{3}{2}$,1-$\sqrt{3}$)∪(1+$\sqrt{3}$,+∞)
故答案为:$a∈(-\frac{3}{2},1-\sqrt{3})∪(1+\sqrt{3},+∞)$
点评 本题考查的知识点是二次函数的图象和性质,熟练掌握二次函数的图象和性质,是解答的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | c>a>b | B. | b>a>c | C. | a>c>b | D. | b>c>a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
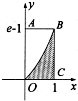 如图所示的阴影部分是由x轴,直线x=1及曲线y=ex-1围成,现向矩形区域OABC内随机投掷一点,则该点落在阴影部分的概率是( )
如图所示的阴影部分是由x轴,直线x=1及曲线y=ex-1围成,现向矩形区域OABC内随机投掷一点,则该点落在阴影部分的概率是( )| A. | $\frac{1}{e}$ | B. | $\frac{1}{e-1}$ | C. | $1-\frac{1}{e}$ | D. | $\frac{e-2}{e-1}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {2,4,6} | B. | {4,6} | C. | {1,3,5} | D. | {1,2,3,4,5,6} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -4 | B. | -1 | C. | 0 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com