
【题目】已知椭圆E:![]() =1(a>b>0)的焦距为2
=1(a>b>0)的焦距为2![]() , 且该椭圆经过点(
, 且该椭圆经过点(![]() ,
,![]() ).
).
(Ⅰ)求椭圆E的方程;
(Ⅱ)经过点P(﹣2,0)分别作斜率为k1 , k2的两条直线,两直线分别与椭圆E交于M,N两点,当直线MN与y轴垂直时,求k1k2的值.
【答案】解:(Ⅰ)由题意得,2c=2![]() ,
,![]() =1;
=1;
解得,a2=4,b2=1;
故椭圆E的方程为![]() +y2=1;
+y2=1;
(Ⅱ)由题意知,当k1=0时,M点的纵坐标为0,
直线MN与y轴垂直,
则点N的纵坐标为0,
故k2=k1=0,这与k2≠k1矛盾.
当k1≠0时,直线PM:y=k1(x+2);
由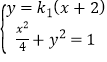 得,
得,
(![]() +4)y2﹣
+4)y2﹣![]() =0;
=0;
解得,yM=![]() ;
;
∴M(![]() ,
,![]() ),
),
同理N(![]() ,
,![]() ),
),
由直线MN与y轴垂直,则![]() =
=![]() ;
;
∴(k2﹣k1)(4k2k1﹣1)=0,
∴k2k1=![]() .
.
【解析】(Ⅰ)由题意得,2c=2![]() ,
, ![]() =1;从而求椭圆E的方程;
=1;从而求椭圆E的方程;
(Ⅱ)由题意知,当k1=0时,M点的纵坐标为0,点N的纵坐标为0,故不成立;当k1≠0时,直线PM:y=k1(x+2);联立方程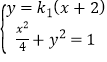 得(
得(![]() +4)y2﹣
+4)y2﹣![]() =0;从而解得yM=
=0;从而解得yM=![]() ;可得M(
;可得M(![]() ,
, ![]() ),N(
),N(![]() ,
, ![]() );从而可得(k2﹣k1)(4k2k1﹣1)=0,从而解得.
);从而可得(k2﹣k1)(4k2k1﹣1)=0,从而解得.
【考点精析】解答此题的关键在于理解椭圆的标准方程的相关知识,掌握椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() .
.


科目:高中数学 来源: 题型:
【题目】设点![]() ,直线
,直线![]() ,点
,点![]() 在直线
在直线![]() 上移动,
上移动, ![]() 是线段
是线段![]() 与
与![]() 轴的交点,
轴的交点, ![]() .
.
(Ⅰ) 求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)直线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,过
,过![]() 的直线
的直线![]() 交轨迹
交轨迹![]() 于
于![]() 两点,
两点,
试探究点![]() 与以
与以![]() 为直径的圆的位置关系,并加以说明.
为直径的圆的位置关系,并加以说明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,M、N是焦点为F的抛物线y2=2px(p>0)上两个不同的点,且线段MN中点A的横坐标为4-![]() ,
,
(1)求|MF|+|NF|的值;
(2)若p=2,直线MN与x轴交于点B点,求点B横坐标的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,EP交圆于E,C两点,PD切圆于D,G为CE上一点且PG=PD,连结DG并延长交圆于点A,作弦AB垂直EP,垂足为F.
(Ⅰ)求证:AB为圆的直径;
(Ⅱ)若AC=BD,求证:AB=ED.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A、B、C所对的边分别为a,b,c,已知cos2C= ![]() .
.
(1)求sinC的值;
(2)当a=2,2sinA=sinC时,求b及c的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某小学随机抽取100名学生,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图),若要从身高在[120,130),[130,140),[140,150]三组内的学生中,用分层抽样的方法选取18人参加一项活动,则从身高在[120,130)内的学生中选取的人数应为( ) 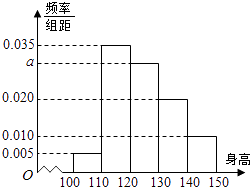
A.10
B.9
C.8
D.7
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com