Question

8．已知边长为2的正方形ABCD的四个顶点在球O的球面上，球O的表面积为64π，则四棱锥O-ABCD的体积为$\frac{4\sqrt{14}}{3}$．

Answer 1

分析 作平面ABCD的垂线OM，则M为正方形中心，求出OA，AM，OM，然后求解四棱锥O-ABCD的体积．

解答 解：过O作OM⊥平面ABCD，垂足为M，则M为正方形ABCD的中心．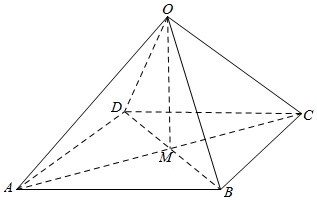
∵正方形ABCD的边长为2，∴AC=2$\sqrt{2}$，AM=$\frac{1}{2}$AC=$\sqrt{2}$，球O的表面积为64π，
∵S_球O=4πr²=64π，∴球O的半径OA=r=4．
∴OM=$\sqrt{{4}^{2}-（{\sqrt{2}）}^{2}}$=$\sqrt{14}$．
则四棱锥O-ABCD的体积为：$\frac{1}{3}×2×2×\sqrt{14}$=$\frac{4\sqrt{14}}{3}$
故答案为：$\frac{4\sqrt{14}}{3}$．

点评 本题考查三棱锥的体积的求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查空间想象能力、推理论证能力，考查化归与转化思想、数形结合思想，是中档题．