
已知 ,
, ,
,
(1)当 时,求
时,求 的单调区间
的单调区间
(2)若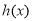 在
在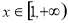 上是递减的,求实数
上是递减的,求实数 的取值范围;
的取值范围;
(3)是否存在实数 ,使
,使 的极大值为3?若存在,求
的极大值为3?若存在,求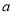 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(1)单调递增区间为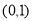 ,单调递减区间为
,单调递减区间为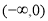 ,
,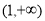 ;(2)
;(2)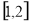 ;(3)不存在实数
;(3)不存在实数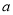 ,使
,使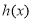 的极大值为3.
的极大值为3.
【解析】
试题分析:(1)先由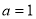 得到h(x)的具体解析表达式,求出其导函数,通过解不等式
得到h(x)的具体解析表达式,求出其导函数,通过解不等式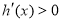 得到其增区间,解不等式
得到其增区间,解不等式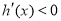 得到其减区间;
得到其减区间;
(2)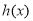 在
在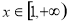 上是递减的等价于
上是递减的等价于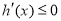 在
在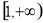 上恒成立,从而通过分离参数转化为
上恒成立,从而通过分离参数转化为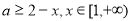 恒成立,从而获得实数
恒成立,从而获得实数 的取值范围;
的取值范围;
(3)先利用导数方法将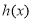 的极大值用a的代数式表达出来,得到
的极大值用a的代数式表达出来,得到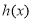 的极大值在
的极大值在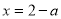 处取到,即
处取到,即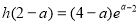 ,令其等于3显然不好判断是否有解,我们可以再利用导数的方法判断出
,令其等于3显然不好判断是否有解,我们可以再利用导数的方法判断出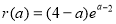 在
在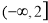 上单调递增,
上单调递增,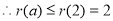 从而可知所求实数a不存在.
从而可知所求实数a不存在.
试题解析:(1) 当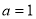 时,
时,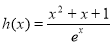 ,则
,则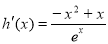
令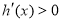 ,解得
,解得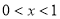 ;令
;令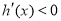 ,解得
,解得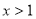 或
或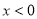
所以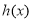 的单调递增区间为
的单调递增区间为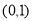 ,单调递减区间为
,单调递减区间为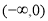 ,
,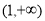
(2)由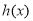 在
在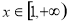 上是递减的,得
上是递减的,得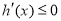 在
在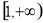 上恒成立,
上恒成立,
即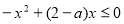 在
在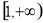 上恒成立,解得
上恒成立,解得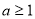 ,又因为
,又因为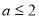 ,
,
所以实数 的取值范围为
的取值范围为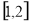
(3)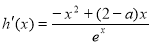 ,令
,令 ,解得
,解得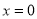 或
或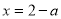

由表可知,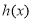 的极大值在
的极大值在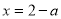 处取到,即
处取到,即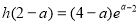 ,
,
设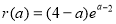 ,则
,则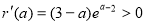 ,所以
,所以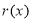 在
在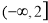 上单调递增
上单调递增
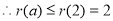 ,所以不存在实数
,所以不存在实数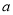 ,使
,使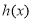 的极大值为3
的极大值为3
考点:1.利用导数求函数的单调区间;2.已知函数的单调性求参数的取值范围;3.函数的极值.


 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:高中数学 来源:2015届山东省高二下学期期中考试理科数学试卷(解析版) 题型:选择题
已知函数 是定义在区间-2,2上的偶函数,当
是定义在区间-2,2上的偶函数,当 时,
时, 是减函数,如果不等式
是减函数,如果不等式 成立,则实数
成立,则实数 的取值范围( )
的取值范围( )
A. B. 1,2 C.
B. 1,2 C.  D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届山东省高二下学期期中考试文科数学试卷(解析版) 题型:选择题
已知定义域为R的函数 ,且对任意实数x,总有
,且对任意实数x,总有 /(x)<3
/(x)<3
则不等式 <3x-15的解集为( )
<3x-15的解集为( )
A.(﹣∞,4)
B.(﹣∞,﹣4)
C.(﹣∞,﹣4)∪(4,﹢∞)
D.(4,﹢∞)
查看答案和解析>>
科目:高中数学 来源:2015届山东省济宁市高二5月质量检测文科数学试卷(解析版) 题型:填空题
关于函数 ,有下列命题
,有下列命题
①由 ,可得
,可得 必是
必是 的整数倍;
的整数倍;
② 的表达式可改写成
的表达式可改写成 ;
;
③ 的图象关于点
的图象关于点 对称;
对称;
④ 的图象关于直线
的图象关于直线 对称.其中正确命题的序号为 .
对称.其中正确命题的序号为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com