
| A. | ($\frac{1}{2}$,+∞) | B. | (-4,+∞) | C. | (-$\frac{5}{8}$,+∞) | D. | [-$\frac{5}{8}$,+∞) |
分析 分离变量,得到a>-$\frac{2}{x}$-$\frac{2}{{x}^{2}}$,利用换元法结合二次函数的闭区间上的最值求解,即可得到a的取值范围.
解答 解:函数f(x)=ax2+2x+2在x∈[1,4]上恒满足f(x)>0,
即a>$-\frac{2x+2}{{x}^{2}}$=-$\frac{2}{x}$-$\frac{2}{{x}^{2}}$,
令t=$\frac{1}{x}$,t∈[$\frac{1}{4}$,1],记m(t)=-2t2-2t,对称轴为t=-$\frac{1}{2}$,
t∈[$\frac{1}{4}$,1],m(t)是减函数,
则m(t)max=m($\frac{1}{4}$)=-$\frac{5}{8}$,∴a>-$\frac{5}{8}$.
故选:C.
点评 考查二次函数的对称轴及二次函数的单调性,以及根据函数的单调性求函数的最小值.


 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 3 | C. | $\frac{7}{2}$ | D. | 7. |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
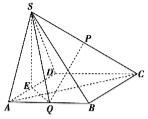 如图,在四棱锥S-ABCD中,底面ABCD为菱形,E、P、Q分别是棱AD、SC、AB的中点,且SE⊥平面ABCD.
如图,在四棱锥S-ABCD中,底面ABCD为菱形,E、P、Q分别是棱AD、SC、AB的中点,且SE⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com