
| A. | $\frac{11}{2}$ | B. | $\frac{16}{3}$ | C. | $2\sqrt{7}$ | D. | 4 |
分析 a1,a3,a13成等比数列,a1=1,可得:${a}_{3}^{2}$=a1a13,即(1+2d)2=1+12d,d≠0,解得d.可得an,Sn.代入$\frac{2{S}_{n}+14}{{a}_{n}+1}$化简利用导数研究单调性即可得出.
解答 解:∵a1,a3,a13成等比数列,a1=1,
∴${a}_{3}^{2}$=a1a13,
∴(1+2d)2=1+12d,d≠0,
解得d=2.
∴an=1+2(n-1)=2n-1.
Sn=$n+\frac{n(n-1)}{2}×2$=n2.
∴$\frac{2{S}_{n}+14}{{a}_{n}+1}$=$\frac{2{n}^{2}+14}{2n}$=n+$\frac{7}{n}$,
利用函数f(x)=x+$\frac{7}{x}$,在$[1,\sqrt{7})$上单调递减,在$(\sqrt{7},+∞)$上单调递增.
∴当n=3时,$\frac{{2{S_n}+14}}{{{a_n}+1}}(n∈N*)$的最小值为$\frac{16}{3}$.
故选:B.
点评 本题考查了等差数列与等比数列的通项公式及其前n项和公式、数列的单调性、利用导数研究函数的单调性,考查了推理能力与计算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
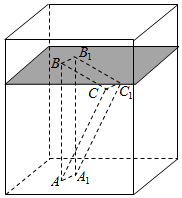 已知三棱柱ABC-A1B1C1,侧棱BB1⊥平面ABC,AB=2,AC=$\sqrt{3}$,AA1=$\frac{1}{4}$,AC⊥BC,将其放入一个水平放置的水槽中,使AA1在水槽底面内,平面ABB1A1与水槽底面垂直,且水面恰好经过棱BB1,现水槽底面出现一个洞,水位下降,则在水位下降过程中,几何体露出水面部分的面积S关于水位下降的高度h的图象大致为( )
已知三棱柱ABC-A1B1C1,侧棱BB1⊥平面ABC,AB=2,AC=$\sqrt{3}$,AA1=$\frac{1}{4}$,AC⊥BC,将其放入一个水平放置的水槽中,使AA1在水槽底面内,平面ABB1A1与水槽底面垂直,且水面恰好经过棱BB1,现水槽底面出现一个洞,水位下降,则在水位下降过程中,几何体露出水面部分的面积S关于水位下降的高度h的图象大致为( )| A. | 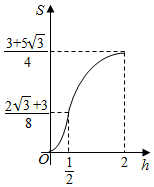 | B. | 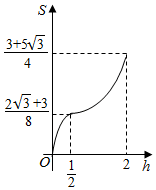 | ||
| C. | 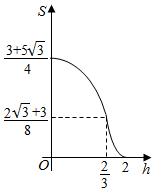 | D. | 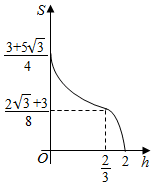 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | -6 | C. | -1 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (4kπ,4kπ+$\frac{π}{2}$)(k∈Z) | B. | (4kπ,4kπ+π)(k∈Z) | C. | (4kπ,4kπ+$\frac{3π}{2}$)(k∈Z) | D. | (4kπ,4kπ+2π)(k∈Z) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com