
分析 (1)根据函数与其反函数的图象关于y=x直线对称;
(2)设h(x)=x,利用导数求得f(x)-h(x)=ex-x的最小值大于0,从而得ex>x,利用导数求得h(x)-g(x)=x-lnx的最小值大于0,从而得x>lnx,这样可证明f(x)的图象恒在g(x)的图象的上方;
(3)根据导数的几何意义得直线的斜率为${e}^{{x}_{1}}$=$\frac{1}{{x}_{2}}$=$\frac{ln{x}_{2}-{e}^{{x}_{1}}}{{x}_{2}-{x}_{1}}$,利用${e}^{{x}_{1}}$>0得:0<x2<1⇒lnx2<0⇒x1>x2+1,可证x1>1.
解答 解:(1)f(x)与g(x)的图象关于直线y=x对称,
(2)证明:g(x)=lnx,设h(x)=x,
令y=f(x)-h(x)=ex-x,
y′=ex-1,
令y′=0,即ex=1,解得x=0,
当x<0时,y′<0,
当x>0时,y′>0,
∴当x=0时,ymin=ex-0=1>0,
∴ex>x,
令y=h(x)-g(x)=x-lnx,
y′=1-$\frac{1}{x}$=$\frac{x-1}{x}$(x>0),
令y′=0,解得:x=1;
当0<x<1时,y′<0,
当x>1,时y′>0,
∴当x=1时,ymin=1-ln1=1>0,
∴x>lnx(x>0)
∴f(x)的图象恒在g(x)的图象的上方;
(3)f′(x)=ex,g′(x)=$\frac{1}{x}$,切点的坐标分别为(x1,${e}^{{x}_{1}}$)(x2,lnx2),
可得方程组:$\left\{\begin{array}{l}{{e}^{{x}_{1}}=\frac{1}{{x}_{2}}}\\{\frac{ln{x}_{2}-{e}^{{x}_{1}}}{{x}_{2}-{x}_{1}}={e}^{{x}_{1}}}\end{array}\right.$,
∵x1>x2>0,
∴${e}^{{x}_{1}}$>1
∴$\frac{1}{{x}_{2}}$>1,
∴0<x2<1,
∴lnx2<0,
又lnx2-${e}^{{x}_{1}}$=${e}^{{x}_{1}}$(x2-x1),
∴lnx2=${e}^{{x}_{1}}$(x2-x1+1)<0,
∴x2-x1+1<0,
x1>x2+1,
∴x1>1.
点评 本题考查了利用导数研究函数的单调性极值与最值、构造函数证明不等式、导数的几何意义、斜率计算公式、指数函数与对数函数的单调性等基础知识与基本技能方法,属于难题.


 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:解答题
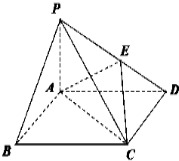 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,PA=AB=2,AD=4,E为线段PD上一点,且$\frac{PE}{PD}$=$\frac{1}{2}$.
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,PA=AB=2,AD=4,E为线段PD上一点,且$\frac{PE}{PD}$=$\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,+∞) | B. | [0,1) | C. | (0,1) | D. | (1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分必要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com