
分析 由偶函数的定义,可得f(-x)=f(x),将x换为x+3,可得f(x+6)=f(x),可得函数为6为周期的函数,f(113.5)=f(0.5)=-$\frac{1}{f(-2.5)}$,由解析式即可得到.
解答 解:∵$f(-x)=f(x),f(x+6)=f(x+3+3)=-\frac{1}{f(x+3)}=f(x)$,
∵f(x)的周期为6,
∴f(113.5)=f(19×6-0.5)=f(-0.5)
=f(0.5)=f(-2.5+3)
=$-\frac{1}{f(-2.5)}=\frac{-1}{2×(-2.5)}=\frac{1}{5}$.
故答案为:$\frac{1}{5}$.
点评 本题考查函数的奇偶性和周期性的判断和运用,考查运算能力,属于中档题.


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
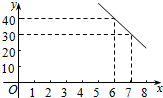 某公司试销一种成本单价为50元/件的新产品,规定试销时销售单价不低于成本单价,又不高于80元/件.经试销调查,发现销售量y(件)与销售单价x(元/件)可近似看作一次函数y=kx+b的关系(如图所示).
某公司试销一种成本单价为50元/件的新产品,规定试销时销售单价不低于成本单价,又不高于80元/件.经试销调查,发现销售量y(件)与销售单价x(元/件)可近似看作一次函数y=kx+b的关系(如图所示).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
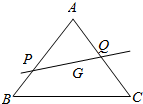 如图,设G为△ABC的重心,过G的直线l分别交AB,AC于P,Q,若$\overrightarrow{AP}$=m$\overrightarrow{AB}$,$\overrightarrow{AQ}$=n$\overrightarrow{AC}$,令$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$
如图,设G为△ABC的重心,过G的直线l分别交AB,AC于P,Q,若$\overrightarrow{AP}$=m$\overrightarrow{AB}$,$\overrightarrow{AQ}$=n$\overrightarrow{AC}$,令$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com