
【题目】已知四棱锥中![]() ,底面
,底面![]() 为菱形,
为菱形,![]() ,
,![]() 平面
平面![]() ,
,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 上的中点,直线
上的中点,直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,点
,点![]() 在
在![]() 上移动.
上移动.
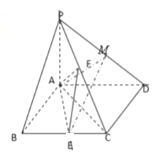
(Ⅰ)证明:无论点![]() 在
在![]() 上如何移动,都有平面
上如何移动,都有平面![]() 平面
平面![]() ;
;
(Ⅱ)求点![]() 恰为
恰为![]() 的中点时,二面角
的中点时,二面角![]() 的余弦值.
的余弦值.
【答案】(Ⅰ)见解析(Ⅱ)![]() .
.
【解析】
(Ⅰ)推导出AE⊥PA,AE⊥AD,从而AE⊥平面PAD,由此能证明无论点F在PC上如何移动,都有平面AEF⊥平面PAD.
(Ⅱ)以A为原点,AE为x轴,AD为y轴,AP为z轴,建立空间直角坐标系,利用向量法能求出二面角C﹣AF﹣E的余弦值.
(Ⅰ)连接![]()
∵底面![]() 为菱形,
为菱形,![]() ,
,
∴![]() 是正三角形,
是正三角形,
∵![]() 是
是![]() 中点,∴
中点,∴![]()
又![]() ,∴
,∴![]()
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() ,又
,又![]()
∴![]() 平面
平面![]() ,又
,又![]() 平面
平面![]()
∴平面![]() 平面
平面![]() .
.
(Ⅱ)由(Ⅰ)得,![]() ,
,![]() ,
,![]() 两两垂直,以
两两垂直,以![]() ,
,![]() ,
,![]() 所在直线分别为
所在直线分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立如图所示的空间直角坐标系,
轴建立如图所示的空间直角坐标系,
∵![]() 平面
平面![]() ,
,
∴![]() 就是
就是![]() 与平面
与平面![]() 所成的角,
所成的角,
在![]() 中,
中,![]() ,即
,即![]() ,
,
设![]() ,则
,则![]() ,得
,得![]() ,
,
又![]() ,设
,设![]() ,则
,则![]() ,
,
所以![]() ,
,
从而![]() ,∴
,∴![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,![]() ,
,
设![]() 是平面
是平面![]() 一个法向量,则
一个法向量,则

 取
取![]() ,得
,得![]()
又![]() 平面
平面![]() ,∴
,∴![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,
∴![]()
![]()
∴二面角![]() 的余弦值为
的余弦值为![]() .
.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源: 题型:
【题目】某同学大学毕业后,决定利用所学专业进行自主创业,经过市场调查,生产一小型电子产品需投入固定成本2万元,每生产![]() 万件,需另投入流动成本
万件,需另投入流动成本![]() 万元,当年产量小于
万元,当年产量小于![]() 万件时,
万件时,![]() (万元);当年产量不小于7万件时,
(万元);当年产量不小于7万件时,![]() (万元).已知每件产品售价为6元,假若该同学生产的商品当年能全部售完.
(万元).已知每件产品售价为6元,假若该同学生产的商品当年能全部售完.
(1)写出年利润![]() (万年)关于年产量
(万年)关于年产量![]() (万件)的函数解析式;(注:年利润=年销售收入-固定成本-流动成本)
(万件)的函数解析式;(注:年利润=年销售收入-固定成本-流动成本)
(2)当年产量约为多少万件时,该同学的这一产品所获年利润最大?最大年利润是多少?
(取![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,a,b,c分别为内角A,B,C的对边,且asin B=-bsin![]() .
.
(1)求A;
(2)若△ABC的面积S=![]() c2,求sin C的值.
c2,求sin C的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,由一块扇形空地![]() ,其中
,其中![]() ,
,![]() 米,计划在此扇形空地区域为学生建灯光篮球运动场,
米,计划在此扇形空地区域为学生建灯光篮球运动场,![]() 区域内安装一批照明灯,点
区域内安装一批照明灯,点![]() 、
、![]() 选在线段
选在线段![]() 上(点
上(点![]() 、
、![]() 分别不与点
分别不与点![]() 、
、![]() 重合),且
重合),且![]() .
.

(1)若![]() 点在距离
点在距离![]() 点
点![]() 米处,求点
米处,求点![]() 、
、![]() 之间的距离;
之间的距离;
(2)为了使运动场地区域最大化,要求![]() 面积尽可能的小,记
面积尽可能的小,记![]() ,请用
,请用![]() 表示
表示![]() 的面积
的面积![]() ,并求
,并求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】指出下列命题是全称量词命题还是存在量词命题,并判断它们的真假.
(1)x∈N,2x+1是奇数;
(2)存在一个x∈R,使![]() =0;
=0;
(3)对任意实数a,|a|>0;
(4)有一个角α,使sinα=![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的最小正周期为
的最小正周期为![]() ,将函数
,将函数![]() 的图像向右平移
的图像向右平移![]() 个单位长度,再向下平移
个单位长度,再向下平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图像.
的图像.
(1)求函数![]() 的单调递增区间;
的单调递增区间;
(2)在锐角![]() 中,角
中,角![]() 的对边分别为
的对边分别为![]() ,若
,若![]() ,
,![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),以坐标原点
),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,且
两点,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com