
如图,△ABC内接于⊙O,AB =AC,直线MN切⊙O于点C,弦BD∥MN,AC与BD相交于点E.
(1)求证:△ABE≌△ACD;
(2)若AB =6,BC =4,求AE.
(1)由边角边即可证得 (2)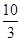
解析试题分析:(Ⅰ)在ΔABE和ΔACD中,
∵ ∠ABE=∠ACD
∠ABE=∠ACD
又,∠BAE=∠EDC ∵BD//MN ∴∠EDC=∠DCN
∵直线是圆的切线,∴∠DCN=∠CAD ∴∠BAE=∠CAD
∴Δ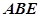
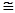 Δ
Δ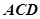 (角、边、角)
(角、边、角)
(Ⅱ)∵∠EBC=∠BCM ∠BCM=∠BDC
∴∠EBC=∠BDC=∠BAC BC=CD=4
又 ∠BEC=∠BAC+∠ABE=∠EBC+∠ABE=∠ABC=∠ACB
∴ BC=BE=4
设AE= ,易证 ΔABE∽ΔDEC
,易证 ΔABE∽ΔDEC
∴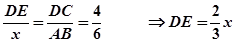 又
又 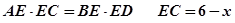
∴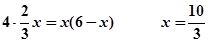
考点:圆內接多边形的性质与判定与圆有关的比例线段
点评:本题考查与圆有关的比例线段,考查圆内接多边形的性质与判定,考查用方程思想解决几何中要求的线段的长,本题是一个应用知识点比较多的题目.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:高中数学 来源: 题型:解答题
如图,⊙O内切△ABC的边于D、E、F,AB=AC,连接AD交⊙O于点H,直线HF交BC的延长线于点G.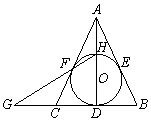
⑴证明:圆心O在直线AD上;
⑵证明:点C是线段GD的中点.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,BA是圆O的直径,延长BA至E,使得AE=AO,过E点作圆O的割线交圆O于D、E,使AD=DC,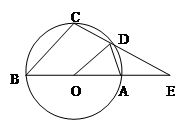
求证: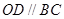 ;
;
若ED=2,求圆O的内接四边形ABCD的周长。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| A.(几何证明选讲选做题)
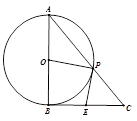 |
| B.(矩阵与变换选做题) 已知M= 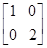 ,N= ,N=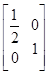 ,设曲线y=sinx在矩阵MN对应的变换作用下得到曲线F,求F的方程. ,设曲线y=sinx在矩阵MN对应的变换作用下得到曲线F,求F的方程. |
| C.(坐标系与参数方程选做题) 在平面直角坐标系xOy中,直线m的参数方程为 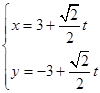 (t为参数);在以O为极点、射线Ox为极轴的极坐标系中,曲线C的极坐标方程为ρsinθ=8cosθ.若直线m与曲线C交于A、B两点,求线段AB的长. (t为参数);在以O为极点、射线Ox为极轴的极坐标系中,曲线C的极坐标方程为ρsinθ=8cosθ.若直线m与曲线C交于A、B两点,求线段AB的长. |
| D.(不等式选做题) |
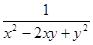 ≥2y+3.
≥2y+3.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分10分)
如图,AD是⊙O的直径,AB是⊙O的切线,M, N是圆上两点,直线MN交AD的延长线于点C,交⊙O的切线于B,BM=MN=NC=1,求AB的长和⊙O的半径.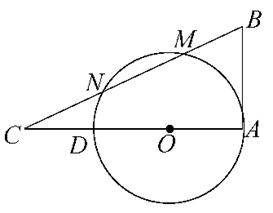
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com