考点:利用导数研究函数的单调性,利用导数研究函数的极值
专题:导数的综合应用
分析:(Ⅰ)求函数的导数,即可求函数f(x)的单调区间和极值;
(Ⅱ)利用函数的单调性,将不等式进行转化即可得到结论.
解答:
解:(Ⅰ)由题知f'(x)=(1-x)e
-x(x∈R),当f'(x)>0时,x<1,当f'(x)<0时,x>1,----(3分)
所以函数f(x)的增区间为(-∞,1),减区间为(1,+∞),
其极大值为
f(1)=,无极小值.-----------(5分)
(Ⅱ)由题知0<x<1,当k≤0时,因为
≤0<x<1,由(1)知函数在(-∞,1)单调递增,
所以
f(x)>f(),符合题意;-------(7分)
当0<k<1时,取x=k,可得f(k)>f(1),这与函数在(-∞,1)单调递增不符;(9分)
当k≥1时,因为
≥>1,由(1)知函数f(x)=xe
-x在(1,+∞)单调递减,
所以
f()≤f(),即只需证
f(x)>f(),即证
xe-x>e-,
同时取对数得ln(xe
-x)>ln(
e-),
即lnx+lne
-x>ln
+ln
e-,
即
lnx-x>-lnx-,
2lnx-x+>0,令
h(x)=2lnx-x+(0<x<1),
则
h′(x)==-<0对0<x<1恒成立,
所以h(x)为(0,1)上的减函数,所以h(x)>h(1)=0,
所以
f(x)>f(),符合题意.-------(11分)
综上:k∈(-∞,0]∪[1,+∞)为所求.------------(12分)
点评:本题主要考查函数单调性和极值的求解,以及导数与不等式的应用,考查学生的运算能力,综合性较强,难度较大.



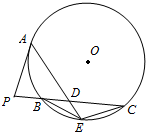 如图,P是⊙O外一点,PA是切线,A为切点,割线PBC与⊙O相交于点B,C,PC=2PA,D为PC的中点,AD的延长线交⊙O于点E,证明:
如图,P是⊙O外一点,PA是切线,A为切点,割线PBC与⊙O相交于点B,C,PC=2PA,D为PC的中点,AD的延长线交⊙O于点E,证明: