
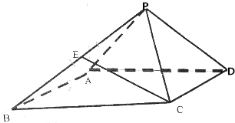
 如图所示,正四棱锥P-ABCD的高为2,AB=3,E为PB的中点.
如图所示,正四棱锥P-ABCD的高为2,AB=3,E为PB的中点.分析 (1)建立如图所示的坐标系,可得所有点的坐标.
(2)利用空间两点间的距离公式,求出CE的长度.
解答 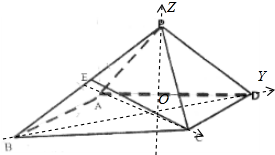 解:(1)建立如图所示的坐标系,则A(-$\frac{3\sqrt{2}}{2}$,0,0),C($\frac{3\sqrt{2}}{2}$,0,0),B(0,-$\frac{3\sqrt{2}}{2}$,0),
解:(1)建立如图所示的坐标系,则A(-$\frac{3\sqrt{2}}{2}$,0,0),C($\frac{3\sqrt{2}}{2}$,0,0),B(0,-$\frac{3\sqrt{2}}{2}$,0),
D(0,$\frac{3\sqrt{2}}{2}$,0),P(0,0,3),E(0,-$\frac{3\sqrt{2}}{4}$,$\frac{3}{2}$);
(2)|CE|=$\sqrt{(\frac{3\sqrt{2}}{2})^{2}+(\frac{3\sqrt{2}}{4})^{2}+(-\frac{3}{2})^{2}}$=$\frac{3\sqrt{14}}{4}$.
点评 本题考查空间向量知识的运用,考查坐标系的建立,正确建立坐标系是关键.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
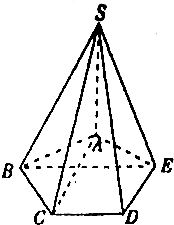 如图,在五棱锥S-ABCDE中,SA⊥底面ABCDE,SA=AB=AE=2,BC=DE=$\sqrt{3}$,∠BAE=∠BCD=∠CDE=120°
如图,在五棱锥S-ABCDE中,SA⊥底面ABCDE,SA=AB=AE=2,BC=DE=$\sqrt{3}$,∠BAE=∠BCD=∠CDE=120°查看答案和解析>>
科目:高中数学 来源: 题型:解答题
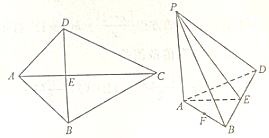 如图,AC为线段BD的垂直平分线,且AE=BE=$\frac{1}{2}$CE=1,现将△BCD沿线段BD翻折到PBD,使二面角P-BD-A为60°.
如图,AC为线段BD的垂直平分线,且AE=BE=$\frac{1}{2}$CE=1,现将△BCD沿线段BD翻折到PBD,使二面角P-BD-A为60°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
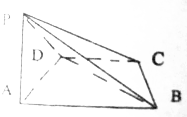 如图,在四棱锥P-ACD中,底面ABCD为等腰梯形,且满足AB∥CD,AD=DC=$\frac{1}{2}$AB=1,PA=$\sqrt{2}$,PA⊥平面ABCD.
如图,在四棱锥P-ACD中,底面ABCD为等腰梯形,且满足AB∥CD,AD=DC=$\frac{1}{2}$AB=1,PA=$\sqrt{2}$,PA⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com