
| A�� | $\sqrt{2}$x��y=0 | B�� | x��$\sqrt{2}$y=0 | C�� | 2x��y=0 | D�� | x��2y=0 |
���� �����Բ��˫���ߵ������ʣ�����������֮���Ĺ�ϵ��Ȼ���Ƴ�a��b��ϵ���������˫���ߵĽ����߷��̣�
��� �⣺a��b��0����ԲC1�ķ���Ϊ$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��C1��������Ϊ��$\frac{\sqrt{{a}^{2}-{b}^{2}}}{a}$��
˫����C2�ķ���Ϊ$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1��C2��������Ϊ��$\frac{\sqrt{{a}^{2}+{b}^{2}}}{a}$��
��C1��C2��������֮��Ϊ$\frac{\sqrt{3}}{2}$��
��$\frac{\sqrt{{a}^{2}-{b}^{2}}}{a}•\frac{\sqrt{{a}^{2}+{b}^{2}}}{a}=\frac{\sqrt{3}}{2}$��
��${��\frac{b}{a}��}^{2}$=$\frac{1}{2}$��$\frac{b}{a}$=$\frac{\sqrt{2}}{2}$��
C2�Ľ����߷���Ϊ��y=$��\frac{\sqrt{2}}{2}x$����x��$\sqrt{2}$y=0
��ѡ��B
���� ���⿼����Բ��˫���ߵĻ������ʣ��������Լ������߷��̵�������֪ʶ�Ŀ��飬������Բ��˫����������֮��Ĺ�ϵ���������ǽ������Ĺؼ���


 ����ѵ�����⿼ϵ�д�
����ѵ�����⿼ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
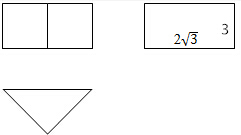 ��һ��������ABC-A1B1C1������ͼ��ͼ��ʾ������ͼ������ͼ��Ϊ���Σ�����ͼΪһ���������Σ�
��һ��������ABC-A1B1C1������ͼ��ͼ��ʾ������ͼ������ͼ��Ϊ���Σ�����ͼΪһ���������Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
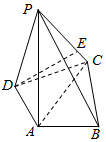 ��ͼ��������P-ABCD�У�PA�͵���ABCD��AC��AB��AD��DC����DAC=60�㣬PA=AC=2��AB=1��
��ͼ��������P-ABCD�У�PA�͵���ABCD��AC��AB��AD��DC����DAC=60�㣬PA=AC=2��AB=1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{2}$ | B�� | $\frac{{\sqrt{2}}}{2}$ | C�� | 1 | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
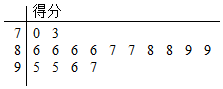 ijУ�Ϳ�չ��ѧϰϰ�����ɡ��������������е��飬�����ȡ��16��ѧ�����в��ԣ��á�10���ơ��Ծ�Ҷͼ��ʽ��¼�����ǵIJ��Է�������ͼ���������÷���������9.5�֣���Ƹ�ѧ����ѧϰϰ�߷dz��á���
ijУ�Ϳ�չ��ѧϰϰ�����ɡ��������������е��飬�����ȡ��16��ѧ�����в��ԣ��á�10���ơ��Ծ�Ҷͼ��ʽ��¼�����ǵIJ��Է�������ͼ���������÷���������9.5�֣���Ƹ�ѧ����ѧϰϰ�߷dz��á����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | t | 4 | 4.5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ����ʱ�� �Ա� | ���� | ���� | �ϼ� |
| ��Ӥ | |||
| ŮӤ | |||
| �ϼ� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com