
| A. | 60 | B. | 72 | C. | 84 | D. | 96 |
分析 根据题意,分3种情况讨论:①、小明的父母的只有1人与小明相邻且父母不相邻,②、小明的父母的只有1人与小明相邻且父母相邻,③、小明的父母都与小明相邻,分别求出每一种情况下的排法数目,由分类计数原理计算可得答案.
解答 解:根据题意,分3种情况讨论:
①、若小明的父母的只有1人与小明相邻且父母不相邻时,
先在其父母中选一人与小明相邻,有C21=2种情况,
将小明与选出的家长看成一个整体,考虑其顺序有A22=2种情况,
当父母不相邻时,需要将爷爷奶奶进行全排列,将整体与另一个家长安排在空位中,有A22×A32=12种安排方法,
此时有2×2×12=48种不同坐法;
②、若小明的父母的只有1人与小明相邻且父母相邻时,
将父母及小明看成一个整体,
小明在一端,有2种情况,考虑父母之间的顺序,有2种情况,则这个整体内部有2×2=4种情况,
将这个整体与爷爷奶奶进行全排列,有A33=6种情况,
此时有2×2×6=24种不同坐法;
③、小明的父母都与小明相邻,即小明在中间,父母在两边,
将3人看成一个整体,考虑父母的顺序,有A22=2种情况,
将这个整体与爷爷奶奶进行全排列,有A33=6种情况,
此时,共有2×6=12种不同坐法;
则一共有48+24+12=84种不同坐法;
故选:C.
点评 本题考查排列、组合的应用,关键是根据题意,进行不重不漏的分类讨论.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:选择题
| A. | -$\frac{22}{17}$ | B. | $\frac{22}{17}$i | C. | $\frac{22}{17}$ | D. | $\frac{3}{17}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分且必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
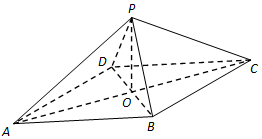 如图,在四棱锥P-ABCD中,四边形ABCD是平行四边形,AD⊥BD且AD=BD,AC∩BD=O,PO⊥平面ABCD.
如图,在四棱锥P-ABCD中,四边形ABCD是平行四边形,AD⊥BD且AD=BD,AC∩BD=O,PO⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x0∉[0,+∞),${e^{x_0}}<1$ | B. | ?x∉[0,+∞),ex<1 | ||
| C. | ?x0∈[0,+∞),${e^{x_0}}<1$ | D. | ?x∈[0,+∞),ex<1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m∥α,α∥β则m∥β | B. | m∥α,m∥n则n∥α | C. | 若m∥α,n⊥α则m⊥n | D. | 若m∥α,n?α则m∥n |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com