
| A. | ①④ | B. | ②④ | C. | ①③ | D. | ②③ |
分析 对4个选项分别进行判断,即可得出结论.
解答 解:①从匀速传递的产品生产流水线上,质检员每20分钟从中抽取一件产品进行某项指标检测,这样的抽样是系统抽样,故①不正确,
②对于两个相关随机变量x,y而言,点P($\overline{x}$,$\overline{y}$)在其回归直线上,正确;
③在回归直线方程$\stackrel{∧}{y}$=0.2x+12中,当解释变量x每增加一个单位时,预报变量$\stackrel{∧}{y}$平均增加0.2个单位,正确.
④两个随机变量相关性越强,则相关系数的绝对值越接近于1;两个随机变量相关性越弱,则相关系数的绝对值越接近于0,故不正确.
故选:D.
点评 本题以命题的真假判断为载体,考查了抽样方法,相关系数,回归分析,独立性检验等知识点,难度不大,属于基础题.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ①④ | D. | ③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
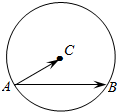 如图,定圆C的半径为4,A为圆C上的一个定点,B为圆C上的动点,若点A,B,C不共线,且$|{\overrightarrow{AB}-t\overrightarrow{AC}}|≥|{\overrightarrow{BC}}|$对任意的t∈(0,+∞)恒成立,则$\overrightarrow{AB}•\overrightarrow{AC}$=16.
如图,定圆C的半径为4,A为圆C上的一个定点,B为圆C上的动点,若点A,B,C不共线,且$|{\overrightarrow{AB}-t\overrightarrow{AC}}|≥|{\overrightarrow{BC}}|$对任意的t∈(0,+∞)恒成立,则$\overrightarrow{AB}•\overrightarrow{AC}$=16.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(b)>f(-$\frac{9}{10}$) | B. | f(b)>0 | C. | f(b)>f($\frac{3}{2}$) | D. | f(b)<f($\frac{3}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 上市时间x天 | 4 | 10 | 36 |
| 市场价y元 | 90 | 51 | 90 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com