
【题目】当x∈[0,1]时,下列关于函数y=![]() 的图象与
的图象与![]() 的图象交点个数说法正确的是( )
的图象交点个数说法正确的是( )
A. 当![]() 时,有两个交点B. 当
时,有两个交点B. 当![]() 时,没有交点
时,没有交点
C. 当![]() 时,有且只有一个交点D. 当
时,有且只有一个交点D. 当![]() 时,有两个交点
时,有两个交点
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:高中数学 来源: 题型:
【题目】某校高一年级学生全部参加了体育科目的达标测试,现从中随机抽取40名学生的测试成绩,整理数据并按分数段![]() 进行分组,假设同一组中的每个数据可用该组区间的中点值代替,则得到体育成绩的折线图(如下):
进行分组,假设同一组中的每个数据可用该组区间的中点值代替,则得到体育成绩的折线图(如下):

(Ⅰ)体育成绩大于或等于70分的学生常被称为“体育良好”.已知该校高一年级有1000名学生,试估计高一全年级中“体育良好”的学生人数;
(Ⅱ)为分析学生平时的体育活动情况,现从体育成绩在![]() 和
和![]() 的样本学生中随机抽取2人,求在抽取的2名学生中,至少有1人体育成绩在
的样本学生中随机抽取2人,求在抽取的2名学生中,至少有1人体育成绩在![]() 的概率;
的概率;
(Ⅲ)假设甲、乙、丙三人的体育成绩分别为![]() 且分别在
且分别在![]() 三组中,其中
三组中,其中![]() 当数据
当数据![]() 的方差
的方差![]() 最小时,写出
最小时,写出![]() 的值.(结论不要求证明)
的值.(结论不要求证明)
(注: ![]() ,其中
,其中![]() 为数据
为数据![]() 的平均数)
的平均数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“绿水青山就是金山银山”的生态文明发展理念已经深入人心,这将推动新能源汽车产业的迅速发展.下表是近几年我国某地区新能源乘用车的年销售量与年份的统计表:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
销量(万台) | 8 | 10 | 13 | 25 | 24 |
某机构调查了该地区30位购车车主的性别与购车种类情况,得到的部分数据如下表所示:
购置传统燃油车 | 购置新能源车 | 总计 | |
男性车主 | 6 | 24 | |
女性车主 | 2 | ||
总计 | 30 |
(1)求新能源乘用车的销量![]() 关于年份
关于年份![]() 的线性相关系数
的线性相关系数![]() ,并判断
,并判断![]() 与
与![]() 是否线性相关;
是否线性相关;
(2)请将上述![]() 列联表补充完整,并判断是否有
列联表补充完整,并判断是否有![]() 的把握认为购车车主是否购置新能源乘用车与性别有关;
的把握认为购车车主是否购置新能源乘用车与性别有关;
(3)若以这30名购车车主中购置新能源乘用车的车主性别比例作为该地区购置新能源乘用车的车主性别比例,从该地区购置新能源乘用车的车主中随机选取50人,记选到女性车主的人数为X,求X的数学期望与方差.
参考公式: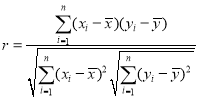 ,
,![]() ,其中
,其中![]() .
.![]() ,若
,若![]() ,则可判断
,则可判断![]() 与
与![]() 线性相关.
线性相关.
附表:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某乡镇为了发展旅游行业,决定加强宣传,据统计,广告支出费![]() 与旅游收入
与旅游收入![]() (单位:万元)之间有如下表对应数据:
(单位:万元)之间有如下表对应数据:
| 2 | 4 | 5 | 6 | 8 |
| 30 | 40 | 60 | 50 | 70 |
(1)求旅游收入![]() 对广告支出费
对广告支出费![]() 的线性回归方程
的线性回归方程![]() ,若广告支出费
,若广告支出费![]() 万元,预测旅游收入;
万元,预测旅游收入;
(2)在已有的五组数据中任意抽取两组,根据(1)中的线性回归方程,求至少有一组数据,其预测值与实际值之差的绝对值不超过![]() 的概率.(参考公式:
的概率.(参考公式: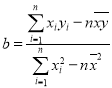 ,
,![]() ,其中
,其中![]() 为样本平均值,参考数据:
为样本平均值,参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,
,![]() 为f(x)的导函数.
为f(x)的导函数.
(1)若a=b=c,f(4)=8,求a的值;
(2)若a≠b,b=c,且f(x)和![]() 的零点均在集合
的零点均在集合![]() 中,求f(x)的极小值;
中,求f(x)的极小值;
(3)若![]() ,且f(x)的极大值为M,求证:M≤
,且f(x)的极大值为M,求证:M≤![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥PABCD的底面ABCD是矩形,PA⊥底面ABCD,点E、F分别是棱PC、PD的中点,则
①棱AB与PD所在直线垂直;
②平面PBC与平面ABCD垂直;
③△PCD的面积大于△PAB的面积;
④直线AE与直线BF是异面直线.
以上结论正确的是________.(写出所有正确结论的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
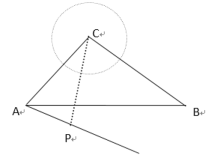
【题目】某工厂C发生爆炸出现毒气泄漏,已知毒气以圆形向外扩散,且半径以每分钟![]() 的速度增大. 一所学校A,位于工厂C南偏西
的速度增大. 一所学校A,位于工厂C南偏西![]() ,且与工厂相距
,且与工厂相距![]() .消防站B位于学校A的正东方向,且位于工厂C南偏东
.消防站B位于学校A的正东方向,且位于工厂C南偏东![]() ,立即以每分钟
,立即以每分钟![]() 的速度沿直线
的速度沿直线![]() 赶往工厂C救援,同时学校组织学生P从A处沿着南偏东
赶往工厂C救援,同时学校组织学生P从A处沿着南偏东![]() 的道路,以每分钟
的道路,以每分钟![]() 的速度进行安全疏散(与爆炸的时间差忽略不计).要想在消防员赶往工厂的时间内(包括消防员到达工厂的时刻),保证学生的安全,学生撤离的速度应满足什么要求?
的速度进行安全疏散(与爆炸的时间差忽略不计).要想在消防员赶往工厂的时间内(包括消防员到达工厂的时刻),保证学生的安全,学生撤离的速度应满足什么要求?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 过点
过点![]() ,过坐标原点
,过坐标原点![]() 作两条互相垂直的射线与椭圆
作两条互相垂直的射线与椭圆![]() 分别交于
分别交于![]() ,
,![]() 两点.
两点.
(1)证明:当![]() 取得最小值时,椭圆
取得最小值时,椭圆![]() 的离心率为
的离心率为![]() .
.
(2)若椭圆![]() 的焦距为2,是否存在定圆与直线
的焦距为2,是否存在定圆与直线![]() 总相切?若存在,求定圆的方程;若不存在,请说明理由.
总相切?若存在,求定圆的方程;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com