
分析 (1)当m=-6时,方程C:x2+y2-2x-4y+m=0,可化为(x-1)2+(y-2)2=11,即可求得圆心和半径;
(2)利用圆心(1,2)到直线l:x+2y-4=0的距离公式可求得圆心到直线距离d,利用圆的半径、弦长之半、d构成的直角三角形即可求得m的值.
解答 解:(1)当m=-6时,方程C:x2+y2-2x-4y+m=0,可化为(x-1)2+(y-2)2=11,
圆心坐标为(1,2),半径为$\sqrt{11}$;
(2)∵(x-1)2+(y-2)2=5-m,
∴圆心(1,2)到直线l:x+2y-4=0的距离d=$\frac{1}{\sqrt{5}}$,
又圆(x-1)2+(y-2)2=5-m的半径r=$\sqrt{5-m}$,$|{MN}|=\frac{4}{{\sqrt{5}}}$,
∴($\frac{2}{\sqrt{5}}$)2+($\frac{1}{\sqrt{5}}$)2=5-m,得m=4.
点评 本题考查圆的方程,考查直线与圆的位置关系,考查学生的计算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | k≥$\frac{5}{4}$ | B. | k>-$\frac{5}{4}$ | C. | k≤-$\frac{5}{4}$ | D. | k<-$\frac{5}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
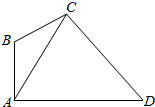 在如图所示的四边形ABCD中,已知AB⊥AD,∠ABC=120°,∠ACD=60°,AD=2$\sqrt{3}$,设∠ACB=θ,点C到AD的距离为h.
在如图所示的四边形ABCD中,已知AB⊥AD,∠ABC=120°,∠ACD=60°,AD=2$\sqrt{3}$,设∠ACB=θ,点C到AD的距离为h.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若非p是q的必要条件,则p是非q的充分条件 | |
| B. | “x>2”是“$\frac{1}{x}<\frac{1}{2}$”的充分不必要条件 | |
| C. | 命题“?x∈R,x2-x≥0”的否定是“?x∈R,x2-x<0” | |
| D. | 若p且q为假命题,则p,q均为假命题 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com