
【题目】如图.已知等腰梯形ABCD中,AB∥CD,AD=AB=![]() CD,M是的CD的中点.N是AC与BM的交点,将△BCM沿BM向上翻折成△BPM,使平面BPM⊥平面ABMD
CD,M是的CD的中点.N是AC与BM的交点,将△BCM沿BM向上翻折成△BPM,使平面BPM⊥平面ABMD
(I)求证:AB⊥PN.
(Ⅱ)若E为PA的中点.求证:EN∥平面PDM.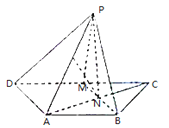
【答案】证明:(1)连结AM,
∵M是的CD的中点,AB=![]() CD,AB∥CD,
CD,AB∥CD,
∴四边形ABCM是平行四边形,四边形ABMD是平行四边形,
∴N是BM的中点,BM=AD,又∵AD=BC,
∴△BCM是等边三角形,即△PBM是等边三角形.
∴PN⊥BM,∵平面PBM⊥平面ABMD,平面PBM∩平面ABMD=BM,PN平面PBM,
∴PN⊥平面ABMD,∵AB平面ABMD,
∴AB⊥PN.
(2)连结PC,∵E是PA的中点,N是AC的中点,
∴EN∥PC,
∵PC平面PDM,EN平面PDM,
∴EN∥平面PDM.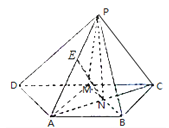
【解析】(1)连结AM,则可证△BCM为等边三角形,从而PN⊥BM,由面面垂直得出PN⊥平面ABMD,故而PN⊥AB;
(2)连结PC,由中位线定理得EN∥PC,故而EN∥平面PDM.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知直线l过点P(0,2),斜率为k,圆Q:x2+y2﹣12x+32=0.
(1)若直线l和圆相切,求直线l的方程;
(2)若直线l和圆交于A、B两个不同的点,问是否存在常数k,使得![]() +
+![]() 与
与![]() 共线?若存在,求出k的值;若不存在,请说明理由.
共线?若存在,求出k的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知中心在原点,焦点在![]() 轴上的椭圆
轴上的椭圆![]() 过点
过点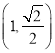 ,离心率为
,离心率为![]() ,
, ![]() ,
, ![]() 是椭圆
是椭圆![]() 的长轴的两个端点(
的长轴的两个端点(![]() 位于
位于![]() 右侧),
右侧),![]() 是椭圆在
是椭圆在![]() 轴正半轴上的顶点.
轴正半轴上的顶点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)是否存在经过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于不同两点
交于不同两点![]() 和
和![]() ,使得向量
,使得向量![]() 与
与![]() 共线?如果存在,求出直线方程;如果不存在,请说明理由.
共线?如果存在,求出直线方程;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为直角坐标系的坐标原点,双曲线
为直角坐标系的坐标原点,双曲线![]()
![]() 上有一点
上有一点![]() (
(![]() ),点
),点![]() 在
在![]() 轴上的射影恰好是双曲线
轴上的射影恰好是双曲线![]() 的右焦点,过点
的右焦点,过点![]() 作双曲线
作双曲线![]() 两条渐近线的平行线,与两条渐近线的交点分别为
两条渐近线的平行线,与两条渐近线的交点分别为![]() ,
, ![]() ,若平行四边形
,若平行四边形![]() 的面积为1,则双曲线的标准方程是( )
的面积为1,则双曲线的标准方程是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某服装销售公司进行关于消费档次的调查,根据每人月均服装消费额将消费档次分为0-500元;500-1000元;1000-1500元;1500-2000元四个档次,针对![]() 两类人群各抽取100人的样本进行统计分析,各档次人数统计结果如下表所示:
两类人群各抽取100人的样本进行统计分析,各档次人数统计结果如下表所示:
| 0~ 500元 | 500~ 1000元 | 1000~ 1500元 | 1500~ 2000元 |
A类 | 20 | 50 | 20 | 10 |
B类 | 50 | 30 | 10 | 10 |
月均服装消费额不超过1000元的人群视为中低消费人群,超过1000元的视为中高收入人群.
(Ⅰ)从![]() 类样本中任选一人,求此人属于中低消费人群的概率;
类样本中任选一人,求此人属于中低消费人群的概率;
(Ⅱ)从![]() 两类人群中各任选一人,分别记为甲、乙,估计甲的消费档次不低于乙的消费档次的概率;
两类人群中各任选一人,分别记为甲、乙,估计甲的消费档次不低于乙的消费档次的概率;
(Ⅲ)以各消费档次的区间中点对应的数值为该档次的人均消费额,估计![]() 两类人群哪类月均服装消费额的方差较大(直接写出结果,不必说明理由).
两类人群哪类月均服装消费额的方差较大(直接写出结果,不必说明理由).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合M={x|0≤x≤2},N={y|0≤y≤2},从M到N有四种对应如图所示: 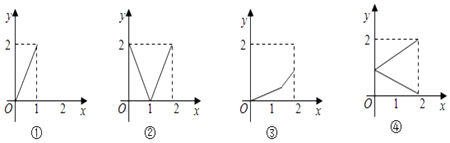
其中能表示为M到N的映射关系的有(请填写符合条件的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com