
【题目】已知直线l过点P(0,2),斜率为k,圆Q:x2+y2﹣12x+32=0.
(1)若直线l和圆相切,求直线l的方程;
(2)若直线l和圆交于A、B两个不同的点,问是否存在常数k,使得![]() +
+![]() 与
与![]() 共线?若存在,求出k的值;若不存在,请说明理由.
共线?若存在,求出k的值;若不存在,请说明理由.
【答案】解:(1)将圆的方程化简,得:(x﹣6)2+y2=4,圆心Q(6,0),半径r=2.
设直线l的方程为:y=kx+2,故圆心到直线l的距离d=![]() =
=![]() .
.
因为直线l和圆相切,故d=r,即![]() =2,解得k=0或k=﹣
=2,解得k=0或k=﹣![]() .
.
所以,直线l的方程为y=2或3x+4y﹣8=0.
(2)将直线l的方程和圆的方程联立,消y得:(1+k2)x2+4(k﹣3)x+36=0,
因为直线l和圆相交,故△=[4(k﹣3)]2﹣4×36×(1+k2)>0,解得﹣![]() <k<0.
<k<0.
设A(x1 , y1)、B(x2 , y2),则有:x1+x2=![]() ;x1x2=
;x1x2=![]()
而y1+y2=kx1+2+kx2+2=k(x1+x2)+4,![]() +
+![]() =(x1+x2 , y1+y2),
=(x1+x2 , y1+y2),![]() =(6,﹣2).
=(6,﹣2).
因为![]() +
+![]() 与
与![]() 共线,所以﹣2×(x1+x2)=6×(y1+y2).
共线,所以﹣2×(x1+x2)=6×(y1+y2).
即(1+3k)(x1+x2)+12=0,代入得(1+3k)[﹣![]() ]+12=0,解得k=﹣
]+12=0,解得k=﹣![]() .
.
又因为﹣![]() <k<0,所以没有符合条件的常数k.
<k<0,所以没有符合条件的常数k.
【解析】(1)确定圆的圆心与半径,设出直线方程,利用直线l和圆相切,建立方程,即可求得结论;
(2)将直线l的方程和圆的方程联立,利用韦达定理,及![]() +
+![]() 与
与![]() 共线,结合根的判别式,可得结论.
共线,结合根的判别式,可得结论.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:高中数学 来源: 题型:
【题目】已知圆C过点(1,2)和(2,1),且圆心在直线x+y﹣4=0上.
(Ⅰ)求圆C的方程;
(Ⅱ)若一束光线l自点A(﹣3,3)发出,射到x轴上,被x轴反射到圆C上,若反射点为M(a,0),求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (
(![]() )的左、右焦点分别为
)的左、右焦点分别为![]() ,
, ![]() ,点
,点 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)是否存在斜率为2的直线![]() ,使得当直线
,使得当直线![]() 与椭圆
与椭圆![]() 有两个不同交点
有两个不同交点![]() 时,能在直线
时,能在直线![]() 上找到一点
上找到一点![]() ,在椭圆
,在椭圆![]() 上找到一点
上找到一点![]() ,满足
,满足![]() ?若存在,求出直线
?若存在,求出直线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从1开始的自然数按如图所示的规则排列,现有一个三角形框架在图中上下或左右移动,使每次恰有九个数在此三角形内,则这九个数的和可以为( )
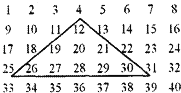
A.2097 B.2112 C.2012 D.2090
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图.已知等腰梯形ABCD中,AB∥CD,AD=AB=![]() CD,M是的CD的中点.N是AC与BM的交点,将△BCM沿BM向上翻折成△BPM,使平面BPM⊥平面ABMD
CD,M是的CD的中点.N是AC与BM的交点,将△BCM沿BM向上翻折成△BPM,使平面BPM⊥平面ABMD
(I)求证:AB⊥PN.
(Ⅱ)若E为PA的中点.求证:EN∥平面PDM.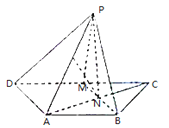
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点![]() ,直线
,直线![]() ,点
,点![]() 在直线
在直线![]() 上移动,
上移动, ![]() 是线段
是线段![]() 与
与![]() 轴的交点,
轴的交点, ![]() .
.
(Ⅰ) 求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)直线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,过
,过![]() 的直线
的直线![]() 交轨迹
交轨迹![]() 于
于![]() 两点,
两点,
试探究点![]() 与以
与以![]() 为直径的圆的位置关系,并加以说明.
为直径的圆的位置关系,并加以说明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com