
分析 根据题意,设计的程序框图应为不等式ax+b<0(a,b∈R)解的运算程序,需要分别分析a>0,a<0,a=0时的解,以及判断b是否为零.注意对a,b的讨论;写程序时要注意IF语句的嵌套.
解答 解:流程图如下: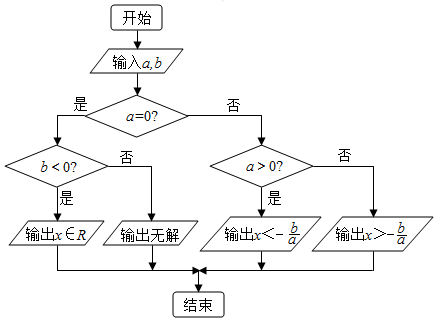
程序如下:
INPUT a,b∈
IF a=0 THEN
IF b<0 THEN PRINT“任意实数”ELSE PRINT“无解”
ELSE IF a>0 THEN PRINT“x<“;-b/a
ELSE PRINT“x>“;-b/a
END IF
END IF
END IF
END
点评 本题考查了程序框图的画法与程序的编写,通过对已知题目的分析,设计解决实际问题的框图,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{6}$海里 | B. | $\sqrt{3}$海里 | C. | 2$\sqrt{3}$海里 | D. | 3海里 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
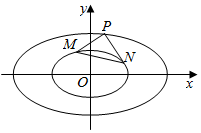 已知椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)过点A($\sqrt{2}$,0),且离心率e=$\frac{\sqrt{2}}{2}$.
已知椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)过点A($\sqrt{2}$,0),且离心率e=$\frac{\sqrt{2}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com