
如图,在半径为30 cm的半圆形(O为圆心)铝皮上截取一块矩形材料ABCD,其中点A,B在直径上,点C,D在圆周上.

(1)怎样截取才能使截得的矩形ABCD的面积最大?并求最大面积.
(2)若将所截得的矩形铝皮 ABCD卷成一个以AD为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),应怎样截取,才能使做出的圆柱形罐子体积最大
ABCD卷成一个以AD为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),应怎样截取,才能使做出的圆柱形罐子体积最大 ?并求最大体积.
?并求最大体积.
(1)(法一)连接OC.
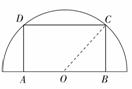
设BC=x,矩形ABCD的面积为S,
则AB=2 ,其中0<x<30.
,其中0<x<30.
所以S=2x
 =2
=2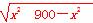 ≤x2+(900-x2)=900,
≤x2+(900-x2)=900,
当且仅当x2=900-x2,即x=15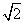 时,S取得最大值为900 cm2.
时,S取得最大值为900 cm2.
(法二)连接OC.设∠BOC=θ,矩形ABCD的面积为S,
则BC=30sin θ,OB=30 cos θ,其中0<θ<
cos θ,其中0<θ< .
.
所以S=AB·BC=2OB·BC=900 sin 2θ.
当sin 2θ=1,即θ=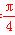 时,
时,
S取最大值为900 cm2,此时BC=15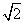 .
.
所以取BC为15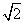 cm时,矩形ABCD的面积最大,最大值为900 cm2.
cm时,矩形ABCD的面积最大,最大值为900 cm2.
(2)(法一)设圆柱底面半径为r,高为x,体积为V,
由AB=2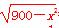 =2πr,得r=
=2πr,得r=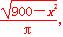 ,
,
所以V=πr2 h=
h= (900x-x3),其中0<x<30.
(900x-x3),其中0<x<30.
由V′= (900-3x2)=0,得x=10
(900-3x2)=0,得x=10 ,
,
因此V= (900x-x3)在(0,10
(900x-x3)在(0,10 )上是增函数,在(10
)上是增函数,在(10 ,30)上是减函数.
,30)上是减函数.
所以当BC=10 时,V取得最大值为
时,V取得最大值为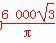 cm3.
cm3.
(法二)连接OC.设∠BOC=θ,圆柱底面半径为r,高为h,体积为V,则圆柱的底面半径为r= ,高h=30sin θ,其中0<θ<
,高h=30sin θ,其中0<θ<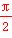 .
.
所以V=πr2h= sin θcos2θ
sin θcos2θ
= (sin θ-sin3θ).
(sin θ-sin3θ).
设t=sin θ(0<t<1),则V= (t-t3).
(t-t3).
由V′= (1-3t2)=0,得t=
(1-3t2)=0,得t=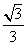 .
.
因此V= (t-t3)在
(t-t3)在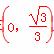 上是增函数,在
上是增函数,在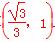 上是减函数,
上是减函数,
所以当t=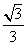 ,即sin θ=
,即sin θ=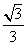 ,BC=10
,BC=10 时,V取得最大值为
时,V取得最大值为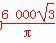 cm3.
cm3.
所以取BC为10 cm时,做出的圆柱形罐子体积最大,最大值为
cm时,做出的圆柱形罐子体积最大,最大值为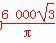 cm3.
cm3.


 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:
某工厂采用高科技改革,在2年内产值的月增长率都是a,则这2年内第2年某月的产值比第1年相应月产值的增长率为( )
A.a12- 1 B.(1+a)12-1
1 B.(1+a)12-1
C.a D.a-1
查看答案和解析>>
科目:高中数学 来源: 题型:
用一根长为12 m的铝合金条做成一个“目”字形窗户的框架(不计损耗),要使这个窗户通过的阳光最充足,则框架的长与宽分别应为____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知a,b,c∈R,函数f(x)=ax2+bx+c.若f(0)=f(4)>f(1),则( )
A.a>0,4a+b=0  B.a<0,4a+b=0
B.a<0,4a+b=0
C.a>0,2a+b=0 D.a<0,2a+b=0
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)由下表给出,
| x | 1 | 2 | 3 |
| f(x) | 2 |
| 1 |
则f(f(2))=______,满足f(f(x))>f(3)的x的值是______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com