练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知函数f(x)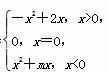＝是奇函数．

    (1)求实数m的值；

    (2)若函数f(x)在区间[－1，a－2]上单调递增，求实数 a的取值范围．


    解析：(1)易知f(1)＝1，f(－1)＝1－m，又∵f(x)是奇函数，∴f(－1)＝－f(1)．∴1－m＝－1.∴m＝2.

    (2)要使f(x)在[－1，a－2]上单调递增，

    结合f(x)的图象知

    ∴1＜a≤3.故实数a的取值范围是(1,3]．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    设M＝{正四棱柱}，N＝{长方体}，Q＝{正方体}，P＝{直四棱柱}，则以下关系式正确的是(　　)

    A．PNMQ　           B．QMNP

    C．PMNQ　           D．QNMP

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    将函数y＝2x＋1的图象按向量a平移得到函数y＝2x＋1的图象，则(　　)

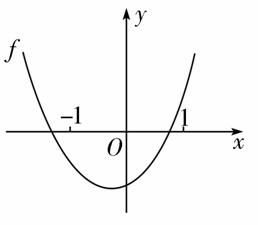
    A．a＝(－1，－1)

    B．a＝(1，－1)

    C．a＝(1,1)

    D．a＝(－1,1)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    定义域为R的四个函数y＝x3，y＝2x，y＝x2＋1，y＝2 sin x中，奇函数的个数是(　　)

    A．4          B．3          C．2         D．1

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设f(x)是定义在R上的奇函数，且当x>0时，f(x)＝1＋2x，则f(－log23)的值等于(　　)

    A．－4　      B．2　     C．3　      D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若曲线f(x)＝、g(x)＝xa在点P(1,1)处的切线分别为l1、l2，且l1⊥l2，则a的值为(　　)

    A．－2         B．2       C.         D．－

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设函数f(x)＝ax－，曲线y＝f(x)在点(2，f(2))处的切线方程为7x－4y－12＝0.

    (1)求y＝f(x)的解析式；

    (2)证明：曲线y＝f(x)上任一点处的切线与直线x＝0和直线y＝x所围成的三角形面积为定值，并求此定值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    对于实数集R上的可导函数f(x)，若满足(x2－3x＋2)f′(x)＜0，则在区间[1,2]上必有(　　)

    A．f(1)≤f(x)≤f(2)       B．f(x)≤f(1)

    C．f(x)≥f(2)             D．f(x)≤f(1)或f(x)≥f(2)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，在半径为30 cm的半圆形(O为圆心)铝皮上截取一块矩形材料ABCD，其中点A，B在直径上，点C，D在圆周上．

    (1)怎样截取才能使截得的矩形ABCD的面积最大？并求最大面积．

    (2)若将所截得的矩形铝皮ABCD卷成一个以AD为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗)，应怎样截取，才能使做出的圆柱形罐子体积最大？并求最大体积．

    查看答案和解析>>

    同步练习册答案