
分析 (1)求导f(x)导数,可得极值点,导数大于0可得增区间;导数小于0可得减区间;进而得到极值;
(2)设切点为(m,n),可得切线的斜率,切线方程,代入(1,0),解方程可得切点,进而得到所求切线方程.
解答 解:(1)f'(x)=3(x2-2),
令f'(x)=0,得${x_1}=-\sqrt{2},{x_2}=\sqrt{2}$,
∴当$x<-\sqrt{2}$或$x>\sqrt{2}$时,f'(x)>0;
当$-\sqrt{2}<x<\sqrt{2}$时,f'(x)<0,
∴f(x)的单调递增区间是$({-∞,-\sqrt{2}})$和$({\sqrt{2},+∞})$,
单调递减区间是$({-\sqrt{2},\sqrt{2}})$;
当x=-$\sqrt{2}$,f(x)有极大值5+4$\sqrt{2}$;当x=$\sqrt{2}$,f(x)有极小值5-4$\sqrt{2}$;
(2)设切点为(m,n),
则切线的斜率为3(m2-2),
切线的方程为y-(m3-6m+5)=3(m2-2)(x-m),
代入(1,0),可得-(m3-6m+5)=3(m2-2)(1-m),
化为(m-1)2(2m+1)=0,
解得m=1或m=-$\frac{1}{2}$,
则斜率为-3或-$\frac{21}{4}$,
可得切线的方程为y=-3x+3或y=-$\frac{21}{4}$x+$\frac{21}{4}$.
点评 本题考查导数的运用:求切线的方程和单调区间、极值,考查化简整理的运算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
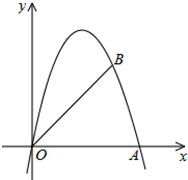 如图,在平面直角坐标系中,己知点O(0,0),A(5,0),B(4,4).
如图,在平面直角坐标系中,己知点O(0,0),A(5,0),B(4,4).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com