
 如图,在平面直角坐标系中,己知点O(0,0),A(5,0),B(4,4).
如图,在平面直角坐标系中,己知点O(0,0),A(5,0),B(4,4).分析 (1)设出抛物线方程,利用已知条件求解即可.
(2)以O、A、B、M为顶点的四边形中,△OAB的面积固定,因此只要另外一个三角形面积最大,则四边形面积即最大.通过①当0<x≤4时,推出x=2时,S△OBM最大值为8,②当4<x≤5时,推出当x=$\frac{9}{2}$时,S△ABM最大值为$\frac{1}{8}$,然后求解四边形的面积最大.
解答 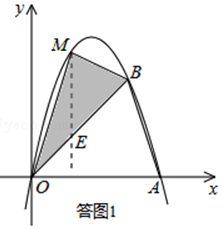 解:(1)∵该抛物线经过点A(5,0),O(0,0),
解:(1)∵该抛物线经过点A(5,0),O(0,0),
∴该抛物线的解析式可设为y=a(x-0)(x-5)=ax(x-5).
∵点B(4,4)在该抛物线上,∴a×4×(4-5)=4.∴a=-1.
∴该抛物线的解析式为y=-x(x-5)=-x2+5x.…2分
(2)以O、A、B、M为顶点的四边形中,△OAB的面积固定,因此只要另外一个三角形面积最大,则四边形面积即最大.
①当0<x≤4时,点M在抛物线OB段上时,如答图1所示.
∵B(4,4),∴易知直线OB的解析式为:y=x.
设M(x,-x2+5x),
过点M作ME∥y轴,交OB于点E,则E(x,x),
∴ME=(-x2+5x)-x=-x2+4x.
S△OBM=S△MEO+S△MEB=$\frac{1}{2}$ME(xE-0)+$\frac{1}{2}$ME(xB-xE)=$\frac{1}{2}$ME•xB=$\frac{1}{2}$ME×4=2ME,
∴S△OBM=-2x2+8x=-2(x-2)2+8
∴当x=2时,S△OBM最大值为8,即四边形的面积最大.….5分
②当4<x≤5时,点M在抛物线AB段上时,图略.可求得直线AB解析式为:y=-4x+20.
设M(x,-x2+5x),过点M作ME∥y轴,交AB于点E,则E(x,-4x+20),
∴ME=(-x2+5x)-(-4x+20)=-x2+9x-20.
S△ABM=S△MEB+S△MEA=$\frac{1}{2}$ME(xE-xB)+$\frac{1}{2}$ME(xA-xE)=$\frac{1}{2}$ME•(xA-xB)=$\frac{1}{2}$ME×1=$\frac{1}{2}$ME,
∴S△ABM=-$\frac{1}{2}$x2+$\frac{9}{2}$x-10=-$\frac{1}{2}$(x-$\frac{9}{2}$)2+$\frac{1}{8}$,
∴当x=$\frac{9}{2}$时,S△ABM最大值为$\frac{1}{8}$,即四边形的面积最大.…8分
比较①②可知,当x=2时,四边形面积最大.
当x=2时,y=-x2+5x=6,∴M(2,6).….9分
点评 本题考查二次函数的解析式的求法,二次函数的简单性质的应用,考查转化思想以及计算能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(0,\;\;\frac{1}{4}]$ | B. | $(0,\;\;\frac{1}{2}]$ | C. | (0,1) | D. | (0,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧¬q | B. | ¬p | C. | p∧q | D. | ¬p∨q |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x<y<z | B. | z<x<y | C. | z<y<x | D. | y<z<x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com