
分析 (1)由an+1=an2-nan-n(n∈N*),且a1=3,分别令 n=1,2,3,4即可求解,进而可猜想;
(2)由(1)可得an=n+2,从而有ann=(n+2)n,利用二项式定理展开后即可证明.
解答 解:(1)n=1时,a2=4;n=2时,a3=5;n=3时,a4=6;n=4时,a5=7;
猜想:an=n+2…(3)
(2)法一:要证$a_n^n≥4{n^n}(n≥2)$成立
只要证(n+2)n≥4nn(n≥2)
只要证(x+2)x≥4xx(x≥2)
只要证xln(x+2)≥ln4+xlnx(x≥2)
即证xln(x+2)-ln4-xlnx≥0(x≥2),
f(x)=xln(x+2)-ln4-xlnx(x≥2)…(6)
$f'(x)=ln(x+2)+\frac{x}{x+2}-lnx-1=ln\frac{x+2}{x}+\frac{x}{x+2}-1$
令$t=\frac{x+2}{x}=1+\frac{2}{x}(1<t≤2)$,则$y=lnt+\frac{1}{t}-1,y'=\frac{1}{t}-\frac{1}{t^2}=\frac{t-1}{t^2}>0$,
所以$y=lnt+\frac{1}{t}-1$在(1,2]上单调递增,所以y>0,即f'(x)>0,
所以f(x)在(2,+∞)单调递增,所以f(x)≥f(2)=0得证.…(10)
法二:令$y={(\frac{a_n}{n})^n}(n≥2),y={(\frac{n+2}{n})^n}={(1+\frac{2}{n})^n}=C_n^0+C_n^1\frac{2}{n}+C_n^2{(\frac{2}{n})^2}+…=1+2+\frac{n(n-1)}{2}•\frac{4}{n^2}+…$
=$5-\frac{2}{n}+…$,
∵n≥2,∴y≥4,即${(\frac{a_n}{n})^n}≥4$,即$a_n^n≥4{n^n}(n≥2)$得证.…(10)
点评 本题主要考查了数列的递推公式在求解数列的通项综的应用及归纳法的应用,解答(2)的关键是二项展开式的应用.


 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
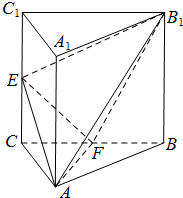 如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC,△ABC为等腰直角三角形,∠BAC=90°,且AB=AA1=1,E,F分别是CC1,BC的中点.
如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC,△ABC为等腰直角三角形,∠BAC=90°,且AB=AA1=1,E,F分别是CC1,BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
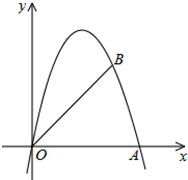 如图,在平面直角坐标系中,己知点O(0,0),A(5,0),B(4,4).
如图,在平面直角坐标系中,己知点O(0,0),A(5,0),B(4,4).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com