
| A. | 9 | B. | 7 | C. | 3+2$\sqrt{2}$ | D. | 1+$\sqrt{2}$ |
分析 通过变形可知问题转化为求$\frac{{x}_{2}-{x}_{3}}{{x}_{1}-{x}_{2}}$+2•$\frac{{x}_{1}-{x}_{2}}{{x}_{2}-{x}_{3}}$的最小值,进而利用基本不等式计算即得结论.
解答 解:∵x1>x2>x3,
∴x1-x2>0,x2-x3>0,x1-x3>0,
又∵$\frac{1}{{{x_1}-{x_2}}}+\frac{2}{{{x_2}-x{\;}_3}}≥\frac{m}{{{x_1}-{x_3}}}$,
∴m≤(x1-x3)($\frac{1}{{x}_{1}-{x}_{2}}$+$\frac{2}{{x}_{2}-{x}_{3}}$)
=$\frac{{x}_{1}-{x}_{2}+{{x}_{2}-x}_{3}}{{x}_{1}-{x}_{2}}$+2•$\frac{{x}_{1}-{x}_{2}+{x}_{2}-{x}_{3}}{{x}_{2}-{x}_{3}}$
=3+$\frac{{x}_{2}-{x}_{3}}{{x}_{1}-{x}_{2}}$+2•$\frac{{x}_{1}-{x}_{2}}{{x}_{2}-{x}_{3}}$,
∵$\frac{{x}_{2}-{x}_{3}}{{x}_{1}-{x}_{2}}$+2•$\frac{{x}_{1}-{x}_{2}}{{x}_{2}-{x}_{3}}$≥2$\sqrt{\frac{{x}_{2}-{x}_{3}}{{x}_{1}-{x}_{2}}•2•\frac{{x}_{1}-{x}_{2}}{{x}_{2}-{x}_{3}}}$=2$\sqrt{2}$,
∴m≤3+2$\sqrt{2}$,
故选:C.
点评 本题考查基本不等式,考查运算求解能力,对表达式的灵活变形是解决本题的关键,注意解题方法的积累,属于中档题.


 步步高达标卷系列答案
步步高达标卷系列答案科目:高中数学 来源: 题型:选择题

| A. | 孵化鸭雏 | B. | 商品鸭饲养 | ||
| C. | 商品鸭收购、育肥、加工 | D. | 羽绒服加工生产体系 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
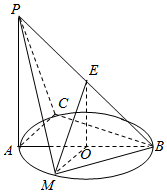 如图所示,PA⊥平面ABC,点C在以AB为直径的⊙O上,∠CBA=30°,PA=AB=2,点E为线段PB的中点,点M在$\widehat{AB}$上,且OM∥AC.
如图所示,PA⊥平面ABC,点C在以AB为直径的⊙O上,∠CBA=30°,PA=AB=2,点E为线段PB的中点,点M在$\widehat{AB}$上,且OM∥AC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | [0,1] | C. | (-∞,1] | D. | (-∞,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥S-ABCD中,底面ABCD是直角梯形,AB垂直于AD和BC,平面SAB⊥底面ABCD,且SA=SB=$\sqrt{2}$,AD=1,AB=2,BC=3.
如图,在四棱锥S-ABCD中,底面ABCD是直角梯形,AB垂直于AD和BC,平面SAB⊥底面ABCD,且SA=SB=$\sqrt{2}$,AD=1,AB=2,BC=3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com