
| A. | y=$\frac{1}{x}$ | B. | y=e-x | C. | y=-x3 | D. | y=lnx |
分析 根据反比例函数的单调性,奇函数图象的对称性,指数函数和对数函数的图象,以及奇函数定义,减函数的定义便可判断每个选项的正误,从而找出正确选项.
解答 解:A.反比例函数$y=\frac{1}{x}$在R上没有单调性,∴该选项错误;
B.$y={e}^{-x}=(\frac{1}{e})^{x}$,图象不关于原点对称,不是奇函数,∴该选项错误;
C.y=-x3的定义域为R,且-(-x)3=-(-x3);
∴该函数为奇函数;
x增大时,x3增大,-x3减小,即y减小,∴该函数在R上单调递减;
∴该选项正确;
D.对数函数y=lnx的图象不关于原点对称,不是奇函数,∴该选项错误.
故选C.
点评 考查反比例函数的单调性,减函数的定义,奇函数的定义,以及奇函数图象的对称性,要熟悉指数函数和对数函数的图象.


 黄冈创优卷系列答案
黄冈创优卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
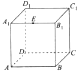 如图,正方体ABCD-A1B1C1D1的棱长为1,E为A1B1的中点,则下列五个命题:
如图,正方体ABCD-A1B1C1D1的棱长为1,E为A1B1的中点,则下列五个命题:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,△ABC是边长为2的等边三角形,△ABD是等腰直角三角形,AD⊥BD,平面ABC⊥平面ABD,且EC⊥平面ABC,EC=1.
如图,△ABC是边长为2的等边三角形,△ABD是等腰直角三角形,AD⊥BD,平面ABC⊥平面ABD,且EC⊥平面ABC,EC=1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-1,2} | B. | {0,1} | C. | {1,2} | D. | {0,1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com