Question

10．如图，△ABC是边长为2的等边三角形，△ABD是等腰直角三角形，AD⊥BD，平面ABC⊥平面ABD，且EC⊥平面ABC，EC=1．
（Ⅰ）证明：DE∥平面ABC；
（Ⅱ）证明：平面ABD⊥平面BDE．

Answer 1

分析 （I）取AB的中点F，连结DF，CF，利用面面垂直的性质得出DF⊥平面ABC，故而DF∥EC，通过计算DF的值可得DF=EC，于是四边形DFCE为平行四边形，得出DE∥CF，得出结论．
（II）利用面面垂直的性质得出CF⊥平面ABD，而CF∥DE．故而DE⊥平面ABD，于是结论得证．

解答 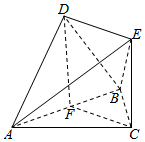证明：（I）取AB的中点F，连结DF，CF，
∵AD=BD，F是AB的中点，
∴DF⊥AB，
又∵平面ABC⊥平面ABD，平面ABC∩平面ABD=AB，DF?平面ABD，
∴DF⊥平面ABC，又∵EC⊥平面ABC，
∴DF∥EC．
∵△ABD是等腰直角三角形，AB=2，
∴DF=$\frac{1}{2}$AB=1，又EC=1，
∴DF=EC，
∴四边形DFCE是平行四边形，
∴DE∥CF，又DE?平面ABC，CF?平面ABC，
∴DE∥平面ABC．
（II）∵△ABC是等边三角形，F是AB的中点，
∴CF⊥AB，
又平面ABC⊥平面ABD，平面ABC∩平面ABD=AB，CF?平面ABC，
∴CF⊥平面ABD，又CF∥ED，
∴DE⊥平面ABD，又DE?平面BDE，
∴平面ABD⊥平面BDE．

点评 本题考查了线面平行，面面垂直的判定，构造平行线与垂线是证明的关键．