
分析 根据圆锥侧面展开图与圆锥的对应关系列方程解出圆锥的底面半径和母线长,计算出圆锥的高.
解答 解:设圆锥的底面半径为r,母线长为l,则$\left\{\begin{array}{l}{l=1}\\{2πr=\frac{2π}{3}×1}\end{array}\right.$,
解得l=1,r=$\frac{1}{3}$.
∴圆锥的高h=$\sqrt{{l}^{2}-{r}^{2}}$=$\frac{2\sqrt{2}}{3}$.
∴圆锥的轴截面面积S=$\frac{1}{2}×2r×h$=$\frac{2\sqrt{2}}{9}$.
故答案为:$\frac{2\sqrt{2}}{9}$.
点评 本题考查了圆锥的结构特征,弧长公式,属于基础题.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 27 | B. | 18 | C. | 36 | D. | 54 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
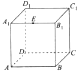 如图,正方体ABCD-A1B1C1D1的棱长为1,E为A1B1的中点,则下列五个命题:
如图,正方体ABCD-A1B1C1D1的棱长为1,E为A1B1的中点,则下列五个命题:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
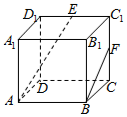 如图,在正方体ABCD-A1B1C1D1中,E,F分别是C1D1,CC1的中点,则异面直线AE与BF所成角的余弦值为( )
如图,在正方体ABCD-A1B1C1D1中,E,F分别是C1D1,CC1的中点,则异面直线AE与BF所成角的余弦值为( )| A. | -$\frac{{5\sqrt{6}}}{18}$ | B. | -$\frac{{\sqrt{5}}}{5}$ | C. | $\frac{{\sqrt{6}}}{5}$ | D. | $\frac{{2\sqrt{5}}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,△ABC是边长为2的等边三角形,△ABD是等腰直角三角形,AD⊥BD,平面ABC⊥平面ABD,且EC⊥平面ABC,EC=1.
如图,△ABC是边长为2的等边三角形,△ABD是等腰直角三角形,AD⊥BD,平面ABC⊥平面ABD,且EC⊥平面ABC,EC=1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com