
| A. | 27 | B. | 18 | C. | 36 | D. | 54 |
分析 由条件利用柯西不等式可得(x2+y2+z2)(25+16+9)≥(5x+4y+3z)2=100,由此求得x2+y2+z2的最小值,再根据基本不等式的性质求出代数式的最小值即可.
解答 解:∵5x+4y+3z=10,利用柯西不等式可得:
(x2+y2+z2)(25+16+9)≥(5x+4y+3z)2=100,
故x2+y2+z2≥2,
∴${9^{x^2}}+{9^{{y^2}+{z^2}}}$≥2$\sqrt{{3}^{2{(x}^{2}{+y}^{2}{+z}^{2})}}$≥2$\sqrt{{3}^{4}}$=18,
当且仅当x2=y2+z2时“=”成立,
故选:B.
点评 本题主要考查柯西不等式应用,考查基本不等式的性质,属于基础题.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | C${\;}_{8}^{3}$ | B. | ${C}_{8}^{4}$ | C. | ${C}_{8}^{5}$ | D. | ${C}_{8}^{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 2015 | D. | 2016 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 18 | B. | 9 | C. | 6 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
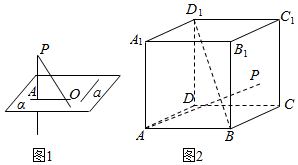
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12 | B. | 6 | C. | 24 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com