
分析 作出不等式组对应的平面区域,结合直线斜率的应用,利用数形结合进行求解即可.
解答 解:作出不等式组对应的平面区域,
$\frac{2y-1}{2x+3}$=$\frac{y-\frac{1}{2}}{x+\frac{3}{2}}$,则对应的几何意义是区域内的点到点(-$\frac{3}{2}$,$\frac{1}{2}$)的斜率,
由图象知AD的斜率最大,
由$\left\{\begin{array}{l}{x=1}\\{x+y=5}\end{array}\right.$得$\left\{\begin{array}{l}{x=1}\\{y=4}\end{array}\right.$,即A(1,4),
此时$\frac{2y-1}{2x+3}$=$\frac{2×4-1}{2+3}$=$\frac{7}{5}$,
故答案为:$\frac{7}{5}$.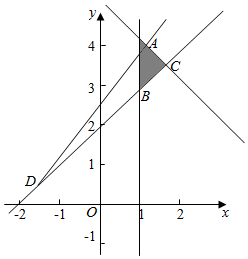
点评 本题主要考查线性规划的应用,利用直线斜率的几何意义是解决本题的关键.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:高中数学 来源: 题型:解答题
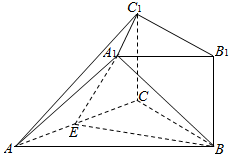 在如图所示的几何体中,四边形BB1C1C是矩形,BB1⊥平面ABC,A1B1∥AB,AB=2A1B1,E是AC的中点.
在如图所示的几何体中,四边形BB1C1C是矩形,BB1⊥平面ABC,A1B1∥AB,AB=2A1B1,E是AC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 中国传统文化中很多内容体现了数学的对称美,如图所示的太极图是由黑白两个鱼形纹组成的圆形图案,充分展现了相互转化、对称统一的形式美、和谐美.给出定义:能够将圆O的周长和面积同时平分的函数称为这个圆的“优美函数”.给出下列命题:
中国传统文化中很多内容体现了数学的对称美,如图所示的太极图是由黑白两个鱼形纹组成的圆形图案,充分展现了相互转化、对称统一的形式美、和谐美.给出定义:能够将圆O的周长和面积同时平分的函数称为这个圆的“优美函数”.给出下列命题:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com