
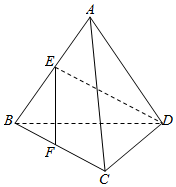
 如图,已知正三角形BCD外一点A满足AB=AD,E,F分别是AB,BC的中点,且EF⊥DE,则∠BAC=$\frac{π}{2}$.
如图,已知正三角形BCD外一点A满足AB=AD,E,F分别是AB,BC的中点,且EF⊥DE,则∠BAC=$\frac{π}{2}$. 分析 取BD的中点M,连结AM,CM,则BD⊥平面ACM,于是BD⊥AC,由中位线定理得EF∥AC,由EF⊥DE,故AC⊥DE,于是AC⊥平面ABD,得出AC⊥AB.
解答 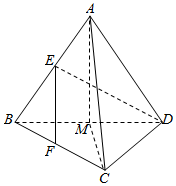 解:取BD的中点M,连结AM,CM,
解:取BD的中点M,连结AM,CM,
∵AB=AD,BC=CD,
∴AM⊥BD,CM⊥BD,又AM?平面ACM,CM?平面ACM,AM∩CM=M,
∴BD⊥平面ACM,∵AC?平面ACM,
∴BD⊥AC,
∵E,F是AB,BC的中点,∴EF∥AC,
∵EF⊥DE,
∴AC⊥DE,
又DE?平面ABD,BD?平面ABD,DE∩BD=D,
∴AC⊥平面ABD,∵AB?平面ABD,
∴AC⊥AB.
故答案为:$\frac{π}{2}$.
点评 本题考查了线面垂直的判定与性质,三线合一是等腰三角形中构造垂线的常用依据,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | {-1,2} | B. | {0,1} | C. | {1,2} | D. | {0,1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2×3n-1 | B. | 2×3n-1-1 | C. | 2×3n-1+1 | D. | 3×2n-1-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
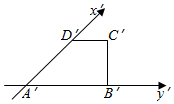 如图,四边形A′B′C′D′是直角梯形,它是四边形ABCD水平放置时的直观图,下底A′B′=20,上底C′D′=10,垂直于底的腰B′C′=10,求B′C′在原平面图形ABCD中的对应线段BC的长度.
如图,四边形A′B′C′D′是直角梯形,它是四边形ABCD水平放置时的直观图,下底A′B′=20,上底C′D′=10,垂直于底的腰B′C′=10,求B′C′在原平面图形ABCD中的对应线段BC的长度.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | |z1|=|$\overline{{z}_{1}}$|=$\sqrt{{{z}_{1}}^{2}}$ | |
| B. | 若|z2|=2,则z2的取值集合为{-2,2,-2i,2i}(i是虚数单位) | |
| C. | 若z12+z22=0,则z1=0或z2=0 | |
| D. | z1$\overline{{z}_{2}}$+$\overline{{z}_{1}}$z2一定是实数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com