
设f(x)=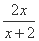 ,x1=1,xn=f(
,x1=1,xn=f(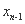 )(n≥2,n∈N+).
)(n≥2,n∈N+).
(1) 求x2,x3,x4的值;
(2) 归纳并猜想{xn}的通项公式;
(3) 用数学归纳法证明你的猜想.
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:高中数学 来源: 题型:
如图,在直三棱柱ABC-A1B1C1中,AB⊥BC,D为棱CC1上任一点.求证:
(1) 直线A1B1∥平面ABD;
(2) 平面ABD⊥平面BCC1B1.

查看答案和解析>>
科目:高中数学 来源: 题型:
在平面直角坐标系xOy中,已知圆O:x2+y2=64,圆O1与圆O相交,圆心为O1(9,0),且圆O1上的点与圆O上的点之间的最大距离为21.
(1) 求圆O1的标准方程;
(2) 过定点P(a,b)作动直线l与圆O,圆O1都相交,且直线l被圆O,圆O1截得的弦长分别为d,d1.若d与d1的比值总等于同一常数λ,求点P的坐标及λ的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com