
在平面直角坐标系xOy中,已知圆O:x2+y2=64,圆O1与圆O相交,圆心为O1(9,0),且圆O1上的点与圆O上的点之间的最大距离为21.
(1) 求圆O1的标准方程;
(2) 过定点P(a,b)作动直线l与圆O,圆O1都相交,且直线l被圆O,圆O1截得的弦长分别为d,d1.若d与d1的比值总等于同一常数λ,求点P的坐标及λ的值.
(1)由题设,得圆O1的半径为4,所以圆O1的标准方程为(x-9)2+y2=16.
(2) 当直线l的斜率存在时,设直线l为y-b=k(x-a),即kx-y-ak+b=0.
则点O,O1到直线l的距离分别为h= ,
,
h1=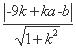 ,
,
从而,d=2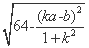 ,
,
d1=2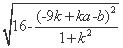 .
.
由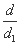 =λ,得
=λ,得
64-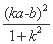 =
=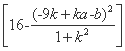 λ2,
λ2,
整理得[64-a2-16λ2+λ2(a-9)2]k2+2b[a-λ2(a-9)]k+64-b2-λ2(16-b2)=0.
由题意,上式对于任意实数k恒成立,
所以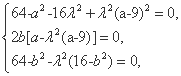
由2b[a-λ2(a-9)]=0,得b=0或a-λ2(a-9)=0.
①如果b=0,则64-16λ2=0,解得λ=2(舍去负值).从而a=6或18,
所以λ=2,点P(6,0),P(18,0).
②如果a-λ2(a-9)=0,显然a=9不满足,从而λ2=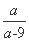 ,
,
所以3a2-43a+192=0.
但Δ=432-4×3×192=-455<0,因此该方程无实数根,舍去.
当点P的坐标为(6,0)时,若直线l的斜率不存在,此时d=4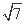 ,d1=2
,d1=2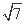 ,所以
,所以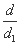 =2,也满足.
=2,也满足.
综上所述,满足题意的λ=2,点P有两个,坐标分别为(6,0)和(18,0).


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
已知函数f(x)=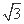 (sin2x-cos2x)-2sinxcosx.
(sin2x-cos2x)-2sinxcosx.
(1) 求函数f(x)的最小正周期;
(2) 设x∈ ,求函数f(x)的值域和单调增区间.
,求函数f(x)的值域和单调增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
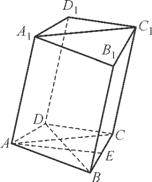
如图,在四棱柱ABCD A1B1C1D1中,已知平面AA1C1C⊥平面ABCD,且AB=BC=CA=
A1B1C1D1中,已知平面AA1C1C⊥平面ABCD,且AB=BC=CA=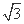 ,AD=CD=1.
,AD=CD=1.
(1) 求证:BD⊥AA1;
(2) 若E为棱BC的中点,求证:AE∥平面DCC1D1.
查看答案和解析>>
科目:高中数学 来源: 题型:
设f(x)=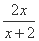 ,x1=1,xn=f(
,x1=1,xn=f(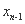 )(n≥2,n∈N+).
)(n≥2,n∈N+).
(1) 求x2,x3,x4的值;
(2) 归纳并猜想{xn}的通项公式;
(3) 用数学归纳法证明你的猜想.
查看答案和解析>>
科目:高中数学 来源: 题型:
在平面直角坐标系xOy中,已知圆C:x2+y2-(6-2m)x-4my+5m2-6m=0,直线l经过点(1,0).若对任意的实数m,定直线l被圆C截得的弦长为定值,则直线l的方程为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
(1) 以极坐标系Ox的极点O为原点、极轴Ox为x轴的正半轴建立平面直角坐标系xOy,并在两种坐标系中取相同的长度单位.将极坐标方程cos θ+ρ2sin θ=1化成直角坐标方程;
(2) 已知曲线C: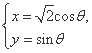 (θ为参数),过点P(2,1)的直线与曲线C交于A,B两点.若PA·PB=
(θ为参数),过点P(2,1)的直线与曲线C交于A,B两点.若PA·PB=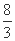 ,求AB的值.
,求AB的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com