练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

     如图,在直三棱柱ABC-A1B1C1中,AB⊥BC,D为棱CC1上任一点.求证:

    (1) 直线A1B1∥平面ABD;

    (2) 平面ABD⊥平面BCC1B1.


     证明略　

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知点A(0,0),B(2,0),C(2,2)在矩阵M=对应的变换作用下得到的对应点分别为A'(0,0),B'(,1),C'(0,2),求矩阵M.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)=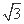(sin2x-cos2x)-2sinxcosx.

    (1) 求函数f(x)的最小正周期;

    (2) 设x∈,求函数f(x)的值域和单调增区间.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知a,b,c分别为△ABC的内角A,B,C所对的边,且acosC+ccosA=2bcosB,求:

    (1) 角B的大小;

    (2) sinA+sinC的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


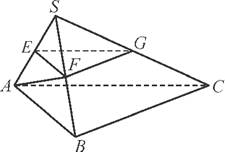
    如图,在三棱锥SABC中,平面SAB⊥平面SBC,AB⊥BC,AS=AB,过点A作AF⊥SB,垂足为F,点E,G分别是棱SA,SC的中点.求证:

    (1) 平面EFG∥平面ABC;

    (2) BC⊥SA.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设a,b是两条不同的直线,α,β是两个不同的平面,现有如下四个命题:

    ①若a⊥b,a⊥α,则b∥α;

    ②若a⊥β,α⊥β,则a∥α;

    ③若a∥α,a⊥β,则α⊥β;

    ④若a⊥b,a⊥α,b⊥β,则α⊥β.

    其中正确的命题序号是　　　　. 

    查看答案和解析>>

    科目：高中数学 来源： 题型：


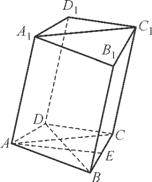
    如图,在四棱柱ABCDA1B1C1D1中,已知平面AA1C1C⊥平面ABCD,且AB=BC=CA=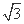,AD=CD=1.

    (1) 求证:BD⊥AA1;

    (2) 若E为棱BC的中点,求证:AE∥平面DCC1D1.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设f(x)=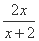,x1=1,xn=f(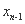)(n≥2,n∈N+).

    (1) 求x2,x3,x4的值;

    (2) 归纳并猜想{xn}的通项公式;

    (3) 用数学归纳法证明你的猜想.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     某种种子每粒发芽的概率都为0.9,现播种了1 000粒,对于没有发芽的种子,每粒需再补种2粒,补种的种子数记为X,则X的数学期望为　　　　.

    查看答案和解析>>

    同步练习册答案