
| A. | $\frac{\sqrt{2}}{4}$ | B. | $\frac{3}{4}$ | C. | -$\frac{1}{4}$ | D. | $\frac{2}{3}$ |
分析 由条件利用正弦定理、余弦定理,诱导公式求得sinB=sin(90°-2C)=cos2C,再利用二倍角的余弦公式求得sin2C=$\frac{3}{4}$,从而求得cosB=sin2C 的值.
解答 解:在△ABC中,∵2b=a+c,∴2sinB=sinA+sinC,
∵A-C=90°,∴2sinB=sin(90°+C)+sinC=cosC+sinC.
再根据A+B+C=180°,可得B=180°-A-C=90°-2C,∴sinB=sin(90°-2C)=cos2C,
∴2cos2C=cosC+sinC,即 2(cosC+sinC )(cosC-sinC )=cosC+sinC,
根据C为锐角,可得cosC-sinC=$\frac{1}{2}$,∴1-sin2C=$\frac{1}{4}$,即sin2C=$\frac{3}{4}$,
则cosB=cos(90°-2C)=sin2C=$\frac{3}{4}$,
故选:B.
点评 本题主要考查正弦定理、余弦定理,诱导公式、二倍角的余弦公式的应用,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | b<a<c | C. | c<b<a | D. | a<c<b |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源:2017届广西南宁二中等校高三8月联考数学(理)试卷(解析版) 题型:解答题
选修4-5:不等式选讲
已知函数 ,
, ;
;
(1)求不等式 的解集;
的解集;
(2)若对任意的 ,
, ,求
,求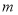 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2017届广西南宁二中等校高三8月联考数学(理)试卷(解析版) 题型:选择题
某同学寒假期间对其30位亲属的饮食习惯进行了一次调查,列出了如下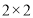 列联表:
列联表:
偏爱蔬菜 | 偏爱肉类 | 合计 | |
50岁以下 | 4 | 8 | 12 |
50岁以上 | 16 | 2 | 18 |
合计 | 20 | 10 | 30 |
则可以说其亲属的饮食习惯与年龄有关的把握为( )
A.90% B.95% C.99% D.99.9%
附:参考公式和临界值表
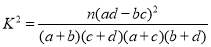
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com