练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    10．设i为虚数单位，复数$\frac{1-i}{i}$=-1-i．

    分析 利用复数的运算法则即可得出．

    解答 解：原式=$\frac{-i（1-i）}{-i•i}$=-1-i．
    故答案为：-1-i．

    点评 本题考查了复数的运算法则，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    20．有2000名网购者在11月11日当天于某购物网站进行网购消费（每人消费金额不超过 1000元），其中有女士1100名，男士900名，该购物网站为优化营销策略，根据性别采用分层抽样的方法从这2000名网购者中抽取200名进行分折，如下表（消费金額卑位：元）
    女士消费情况：
     消费金额 （0.200） 
    [200，400）    		 
    [400.600）    		 
    [600，800）    		 
    [800，1000]
     人数 10 25 35 30 X
    男士消费情况况：
    消费金额（0.200）
    [200，400）
    [400.600）
    [600，800）
    [800.1000]
    人数153025Y5
    （1）计算算x，y的值；在抽出的200名且消费金额在[800，1000]（单位：元）的网购者中随机选出两名发放网购红包，求选出的两名网购者都是男士的概率；
    （2）若消费金额不低于600元的网购者为“网购达人，低于600元的网购者为“非网购达人”根据以上统计数据填写答题卡中的2×2列联表，并冋答能否在犯错误的概率不超过0.05的前提下认为“是否为网购达人与性别有关？”
    附表：
     P（K2≥k0） 0.10 0.05 0.025 0.010 0.005
     k0 2.706 3.841 5.024 6.635 7.879
    （K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$，n=a+b+c+d）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．在平面直角坐标系中，以坐标原点为极点，x轴的非负半轴为极轴建立坐标系．已知点A的极坐标为（$\sqrt{2}$，$\frac{π}{4}$），直线的极坐标方程为ρcos（θ-$\frac{π}{4}$）=a，且点A在直线上．
    （1）求a的值及直线的直角坐标方程；
    （2）圆C的参数方程为$\left\{\begin{array}{l}{x=1+cosα}\\{y=sinα}\end{array}\right.$（α为参数），试判断直线与圆的位置关系．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    18．设n∈N*，（x+3）n展开式的所有项系数和为256，则其二项式系数的最大值为6．（用数字作答）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．正数列{an}的前n项和Sn满足：rSn=anan+1-1，a1=a＞0，常数r∈N．
    （Ⅰ）求证：an+2-an为定值；
    （Ⅱ）若数列{an}是一个周期数列（即存在非零常数T，使an+T=an恒成立），求该数列的最小正周期；
    （Ⅲ）若数列{an}是一个各项为有理数的等差数列，求Sn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

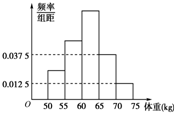    15．为了了解某县今年高考准备报考体育专业的学生的体重情况，将所得的学生体重数据分组整理后，画出了频率分布直方图（如图），已知图中从左到右的前3小组的频率a，b，c恰成等差数列，若抽取的学生人数是48，则第2小组的频数为（　　）
    A．6B．12C．18D．24

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．已知矩阵M=$[\begin{array}{l}{2}&{1}\\{1}&{2}\end{array}]$，β=$[\begin{array}{l}{3}\\{5}\end{array}]$，计算M2β．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．袋中有5个球，其中有彩色球2个．甲、乙二人先后依次从袋中取球，每次取后不放回，规定先取出彩色球者获胜．则甲获胜的概率为$\frac{3}{5}$．（以整数比作答）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．如图，四棱锥P-ABCD中，底面ABCD为菱形，PA⊥底面ABCD，AC=2$\sqrt{2}$，PA=2，$\overrightarrow{PE}$=2$\overrightarrow{EC}$．
    （Ⅰ）证明：PC⊥平面BED；
    （Ⅱ）若直线PD与平面PBC所成角为$\frac{π}{6}$，求二面角A-PB-C的大小．

    查看答案和解析>>

    同步练习册答案