Question

5．已知定义在实数集R上的奇函数f（x），当x∈（0，1）时，f（x）=$\frac{1}{x}$（$\frac{1}{{2}^{x}-1}$+$\frac{1}{2}$）．
（1）求函数f（x）在（-1，1）上的解析式；
（2）判断f（x）的单调性；
（3）判断关于x的方程f（x）=λx²的实根个数．

Answer 1

分析 （1）由题意得f（0）=0，再利用奇函数求当x∈（-1，0）时的解析式即可；
（2）当x∈（0，1）时，可判断$\frac{1}{x}$＞0且在（0，1）上是减函数，$\frac{1}{{2}^{x}-1}$+$\frac{1}{2}$＞0且在（0，1）上是减函数，从而判断函数的单调性；
（3）分λ=0，λ＞0，λ＜0进行讨论，结合函数的图象确定方程的根的个数．

解答 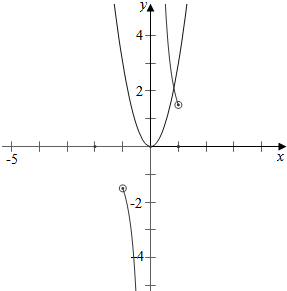解：（1）由题意得，
f（0）=0，
当x∈（-1，0）时，
f（x）=-f（-x）=-[-$\frac{1}{x}$（$\frac{1}{{2}^{-x}-1}$+$\frac{1}{2}$）]
=$\frac{1}{x}$（$\frac{1}{{2}^{-x}-1}$+$\frac{1}{2}$）；
故f（x）=$\left\{\begin{array}{l}{\frac{1}{x}（\frac{1}{{2}^{x}-1}+\frac{1}{2}），0＜x＜1}\\{0，x=0}\\{\frac{1}{x}（\frac{1}{{2}^{-x}-1}+\frac{1}{2}），-1＜x＜0}\end{array}\right.$；
（2）当x∈（0，1）时，
$\frac{1}{x}$＞0且在（0，1）上是减函数，
$\frac{1}{{2}^{x}-1}$+$\frac{1}{2}$＞0且在（0，1）上是减函数，
故f（x）在（0，1）上是减函数；
故f（x）在（0，1），（-1，0）上是减函数．
（3）①当λ=0时，
方程f（x）=λx²=0有且只有一个实根x=0；
②当λ＞0时，作函数y=f（x）与y=λx²的图象如右图，
结合图象可知，
当λ•1²＞1•（1+$\frac{1}{2}$），即λ＞$\frac{3}{2}$时，
关于x的方程f（x）=λx²有两个不同的实根；
当0＜λ≤$\frac{3}{2}$时，
关于x的方程f（x）=λx²有且只有一个实根；
③当λ＜0时，同理可得，
当λ＜-$\frac{3}{2}$时，关于x的方程f（x）=λx²有两个不同的实根；
当-$\frac{3}{2}$≤λ＜0时，关于x的方程f（x）=λx²有且只有一个实根；
综上所述，
当-$\frac{3}{2}$≤λ≤$\frac{3}{2}$时，关于x的方程f（x）=λx²有且只有一个实根；
当λ＜-$\frac{3}{2}$或λ＞$\frac{3}{2}$时，关于x的方程f（x）=λx²有两个不同的实根．

点评 本题考查了函数的奇偶性的应用及函数的单调性的判断与应用，同时考查了数形结合的思想及分类讨论的思想．