练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知抛物线： 的焦点为，过的直线交抛物线于点，当直线的倾斜角是时， 的中垂线交轴于点.

    （1）求的值；

    （2）以为直径的圆交轴于点，记劣弧的长度为，当直线绕点旋转时，求的最大值.

    【答案】（1）（2）

    【解析】试题分析：（1）设出直线的方程为，设，联立直线与抛物线方程，利用韦达定理求出中点坐标，推出中垂线方程，结合的中垂线交轴于点，求出即可；（2）设方程为，代入，求出的距离以及中点为，令，求出的表达式，推出关系式，利用到轴的距离，求出，分离常数即可求得的最大值.

    试题解析：（1） 当的倾斜角为时， 的方程为

    设 得

    得中点为

    中垂线为 代入得

    （2）设的方程为，代入得

    中点为

    令

    到轴的距离

    当时取最小值

    的最大值为

    故的最大值为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】集合U＝R，A＝{x|x2－x－2<0}，B＝{x|y＝ln(1－x)}，则图中阴影部分所表示的集合是( )

    A.{x|x≥1}
    B.{x|1≤x<2}
    C.{x|0<x≤1}
    D.{x|x≤1}

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了解人们对于国家新颁布的“生育二胎放开”政策的热度，现在某市进行调查，随机调查了人，他们年龄大点频数分布及支持“生育二胎”人数如下表：

    年龄

    频数

    支持“生育二胎”

    （Ⅰ）由以上统计数据填下面乘列联表，并问是否有的把握认为以岁为分界点对“生育二胎放开”政策的支持度有差异：

    年龄不低于岁的人数

    年龄低于岁的人数

    合计

    支持

    不支持

    合计

    （Ⅱ）若对年龄在的的被调查人中随机选取两人进行调查，恰好这两人都支持“生育二胎放开”的概率是多少？

    参考数据： ， .

    查看答案和解析>>

    科目：高中数学 来源： 题型：

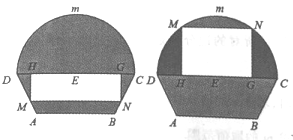
    【题目】如图所示的自动通风设施.该设施的下部是等腰梯形，其中为2米，梯形的高为1米， 为3米，上部是个半圆，固定点为的中点. 是由电脑控制可以上下滑动的伸缩横杆（横杆面积可忽略不计），且滑动过程中始终保持和平行.当位于下方和上方时，通风窗的形状均为矩形（阴影部分均不通风）.

    （1）设与之间的距离为（且）米，试将通风窗的通风面积（平方米）表示成关于的函数；

    （2）当与之间的距离为多少米时，通风窗的通风面积取得最大值？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数， .

    （1）求函数的单调区间；

    （2）若函数在处取得极大值，求正实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设锐角三角形的内角的对边分别为， ．

    （Ⅰ）求的大小；

    （Ⅱ）求的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数的图象与轴相切，且切点在轴的正半轴上.

    （1）求曲线与轴，直线及轴围成图形的面积；

    （2）若函数在上的极小值不大于，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=（sinx+cosx）2-2cos2x，

    （1）求函数f（x）的最小正周期和单调递减区间；

    （2）当x∈时，求f（x）的最大值和最小值

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知二次函数，关于实数的不等式的解集为．

    （1）当时，解关于的不等式： ；

    （2）是否存在实数，使得关于的函数（）的最小值为？若存在，求实数的值；若不存在，说明理由．

    查看答案和解析>>

    同步练习册答案