
分析 函数y=sinx+cos2x=-2sin2x+sinx+1,令t=sinx,则t∈[-1,1],y=-2t2+t+1,结合二次函数的图象和性质,可得答案.
解答 解:函数y=sinx+cos2x=-2sin2x+sinx+1,
令t=sinx,则t∈[-1,1],y=-2t2+t+1,
当t=$\frac{1}{4}$时,函数取最大值$\frac{9}{8}$,
当t=-1时,函数取最小值-2,
故函数的值域为[-2,$\frac{9}{8}$],
故答案为:[-2,$\frac{9}{8}$]
点评 本题考查的知识点是函数的最值及其几何意义,二次函数的图象和性质,三角函数的化简求值,难度中档.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(2)<f(-2)<f(0) | B. | f(0)<f(2)<f(-2) | C. | f(-2)<f(0)<f(2) | D. | f(-)<f(-2)<f(2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | 0 | C. | $\frac{1}{2}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
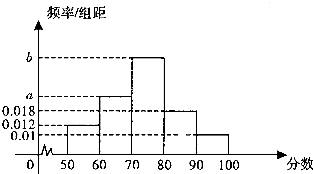
| A. | 0.024 | B. | 0.036 | C. | 0.06 | D. | 0.6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的上、下顶点分别为A,B,右焦点为F,点$P(\frac{{2\sqrt{13}}}{13},\frac{{2\sqrt{39}}}{13})$在椭圆C上,且OP⊥AF.
椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的上、下顶点分别为A,B,右焦点为F,点$P(\frac{{2\sqrt{13}}}{13},\frac{{2\sqrt{39}}}{13})$在椭圆C上,且OP⊥AF.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{5π}{12}$ | C. | $\frac{2π}{3}$ | D. | -$\frac{2π}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com