
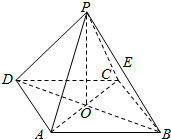
 已知:正四棱锥P-ABCD,O为正方形ABCD的中心,PA与底ABCD所成的角为α,且cosα=$\frac{\sqrt{10}}{5}$.
已知:正四棱锥P-ABCD,O为正方形ABCD的中心,PA与底ABCD所成的角为α,且cosα=$\frac{\sqrt{10}}{5}$.分析 (1)若E为PB的中点,根据线面平行的判定定理证明OE∥DP,即可证明OE∥平面PCD;
(2)根据二面角的定义作出侧面和底面的二面角的平面角,结合三角函数的关系即可求侧面PCD与底面ABCD所成二面角的大小.
解答 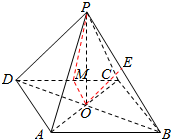 (1)证明:连接OE,
(1)证明:连接OE,
∵E为PB的中点,O为正方形ABCD的中心,
∴OE是三角形PDB的中位线,
则OE∥DP,
∵OE?平面PCD,DP?平面PCD,
∴OE∥平面PCD.
解:(2)取CD中点M,连接MO,PM,依条件可知CD⊥MO,CD⊥PO,则∠PMO为侧面PCD与底面ABCD所成二面角的平面角,
∵PO⊥面ABCD,
∴∠PAO为侧棱PA与底面ABCD所成的角.
∵PA与底ABCD所成的角为α,且cosα=$\frac{\sqrt{10}}{5}$.
即cos∠PAO=$\frac{\sqrt{10}}{5}$.
∴设AB=a,AO=$\frac{\sqrt{2}}{2}$a,
则cos∠PAO=$\frac{AO}{PA}$=$\frac{\frac{\sqrt{2}a}{2}}{PA}$=$\frac{\sqrt{10}}{5}$.
则PA=$\frac{\sqrt{5}}{2}$a,
∴PO=$\sqrt{P{A}^{2}-A{O}^{2}}$=$\sqrt{(\frac{\sqrt{5}a}{2})^{2}-(\frac{\sqrt{2}a}{2})^{2}}$=$\frac{\sqrt{3}}{2}$a,
∵OM=$\frac{a}{2}$,
∴在直角三角形PM0中,tan∠PMO=$\frac{PO}{OM}$=$\frac{\frac{\sqrt{3}}{2}a}{\frac{1}{2}a}$=$\sqrt{3}$.
∴∠PMO=60°.
即侧面PCD与底面ABCD所成二面角的大小是60°.
点评 本题主要考查了线面平行的判定依据二面角及其度量,根据线面平行的判定定理以及二面角的定义通过过巧妙设置辅助线找到二面角是解决本题的关键..


科目:高中数学 来源: 题型:解答题
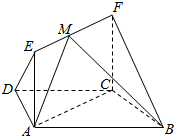 如图,矩形ACFE⊥底面ABCD,底面ABCD为等腰梯形,且AB∥CD,AB=2AD=2CD=2CF.
如图,矩形ACFE⊥底面ABCD,底面ABCD为等腰梯形,且AB∥CD,AB=2AD=2CD=2CF.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
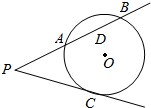 如图,过点P作圆O的切线PC,切点为C,过点P的直线与圆O交于点A,B(PA<PB),且AB的中点为D.
如图,过点P作圆O的切线PC,切点为C,过点P的直线与圆O交于点A,B(PA<PB),且AB的中点为D.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{2\sqrt{2}}}{3}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充要 | D. | 既不充分也不必要 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com