
| A. | 1个 | B. | 2个 | C. | 3 个 | D. | 4个 |
分析 画出f(x)与g(x)的图象,看一下图象之间有多少个交点即可.
解答 解:由题意:$f(x)=\left\{{\begin{array}{l}{2,\;0<x≤10}\\{3,\;10<x≤15}\\{4,\;15<x≤20}\end{array}}\right.$,$g(x)=5sin\frac{π}{60}x$,
函数F(x)=f(x)-g(x)(0<x≤20)的零点个数等价于f(x)=g(x)两个图象的交点.
已知:$f(10)=2,g(10)=2.5>2,f(15)=3,g(15)=5•\frac{{\sqrt{2}}}{2}>3,g(15)<4$,$f(20)=4,g(20)=\frac{{5\sqrt{3}}}{2}>4$.
图象如下: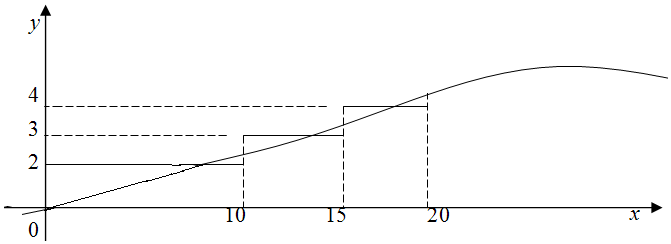
从图象可以看出0<x≤20,f(x)的图象与g(x)两个图象由3个交点.即函数F(x)=f(x)-g(x)由3个零点.
故选C.
点评 本题考查了分段函数的值域以及图象画法与三角函数的画法,两图象的交点问题就是零点的问题.属于基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{12}$ | B. | $\frac{1}{2}$ | C. | $\frac{7}{12}$ | D. | $\frac{5}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 最大值是$\sqrt{2}$,周期是π | B. | 最小值是-2,周期是2π | ||
| C. | 最大值是$\sqrt{2}$,周期是2π | D. | 最小值是-2,周期是π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
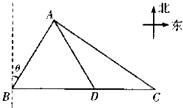 如图,某流动海洋观测船开始位于灯塔B的北偏东$θ(0<θ<\frac{π}{2})$方向,且满足$2{sin^2}(\frac{π}{4}+θ)-\sqrt{3}$cos2θ=1,AB=AD,在接到上级命令后,该观测船从A点位置沿AD方向在D点补充物资后沿BD方向在C点投放浮标,使得C点与A点的距离为4$\sqrt{3}$km,
如图,某流动海洋观测船开始位于灯塔B的北偏东$θ(0<θ<\frac{π}{2})$方向,且满足$2{sin^2}(\frac{π}{4}+θ)-\sqrt{3}$cos2θ=1,AB=AD,在接到上级命令后,该观测船从A点位置沿AD方向在D点补充物资后沿BD方向在C点投放浮标,使得C点与A点的距离为4$\sqrt{3}$km,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $-\frac{1}{3}$ | C. | -3 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com