
| A. | $\frac{5}{12}$ | B. | $\frac{1}{2}$ | C. | $\frac{7}{12}$ | D. | $\frac{5}{2}$ |
分析 先求出基本事件总数N=6×6=36,再由列举法求出θ∈(0,$\frac{π}{2}$)包含的基本事件个数,由此能求出θ∈(0,$\frac{π}{2}$)的概率.
解答 解:∵连续抛掷两次骰子,得到的点数分别为m,n,
∴基本事件总数N=6×6=36,
∵记向量$\overrightarrow{a}$=(m,n),$\overrightarrow{b}$=(1,-1)的夹角为θ,θ∈(0,$\frac{π}{2}$),
∴$\overrightarrow{a}•\overrightarrow{b}$=m-n>0,
∴θ∈(0,$\frac{π}{2}$)包含的基本事件(m,n)有:
(2,1),(3,1),(3,2),(4,1),(4,2),(4,3),(5,1),(5,2),
(5,3),(5,4),(6,1),(6,2),(6,3),(6,4),(6,5),
共有M=15个,
∴θ∈(0,$\frac{π}{2}$)的概率p=$\frac{M}{N}$=$\frac{15}{36}=\frac{5}{12}$.
故选:A.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.


科目:高中数学 来源: 题型:解答题
 如图,已知点C是以AB为直径的圆O上一点,CG垂直于AB,垂足为G,过B点做圆O的切线,交直线AC于点D,点E是CG的中点,连接并延长AE交BD于点F,求证:
如图,已知点C是以AB为直径的圆O上一点,CG垂直于AB,垂足为G,过B点做圆O的切线,交直线AC于点D,点E是CG的中点,连接并延长AE交BD于点F,求证:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
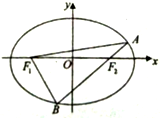 已知F1、F2是椭圆$\frac{x^2}{λ+1}+\frac{y^2}{λ}=1\;(0<λ<1)$在左、右焦点,直线AB经过F2交椭圆于A、B两点(A点在x轴上方),连结AF1、BF1.
已知F1、F2是椭圆$\frac{x^2}{λ+1}+\frac{y^2}{λ}=1\;(0<λ<1)$在左、右焦点,直线AB经过F2交椭圆于A、B两点(A点在x轴上方),连结AF1、BF1.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3 个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 在研究身高和体重的相关性中,R2=0.64,表明身高解释了$\begin{array}{l}64%\end{array}$的体重变化 | |
| B. | 若a,b,c∈R,有(ab)•c=a•(bc),类比此结论,若向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$,有($\overrightarrow{a}$•$\overrightarrow{b}$)•$\overrightarrow{c}$=$\overrightarrow{a}$•($\overrightarrow{b}$•$\overrightarrow{c}$), | |
| C. | 在吸烟与患肺癌是否相关的判断中,由独立性检验可知,在犯错误的概率不超过0.01的前提下,认为吸烟与患肺癌有关系,那么在100个吸烟的人中,必有99个人患肺癌 | |
| D. | 若a,b∈R,则a-b>0⇒a>b,类比推出若a,b∈C,则a-b>0⇒a>b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com