
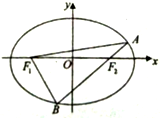
 已知F1、F2是椭圆$\frac{x^2}{λ+1}+\frac{y^2}{λ}=1\;(0<λ<1)$在左、右焦点,直线AB经过F2交椭圆于A、B两点(A点在x轴上方),连结AF1、BF1.
已知F1、F2是椭圆$\frac{x^2}{λ+1}+\frac{y^2}{λ}=1\;(0<λ<1)$在左、右焦点,直线AB经过F2交椭圆于A、B两点(A点在x轴上方),连结AF1、BF1.分析 (1)利用c=$\sqrt{λ+1-λ}$,可得焦点.由椭圆的定义可得:|AF1|+|AF2|=|BF1|+|BF2|=2a,即可得出.
(2)设直线AB的方程为:my=x-1,A(x1,y1),B(x2,y2).与椭圆方程联立化为:(λm2+λ+1)y2+2λmy-λ2=0,利用根与系数的关系可得|y1-y2|=$\sqrt{({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}}$.可得△ABF1面积S=$\frac{1}{2}×2c×$|y1-y2|,化简利用基本不等式的性质即可得出.
解答 解:(1)由椭圆$\frac{x^2}{λ+1}+\frac{y^2}{λ}=1\;(0<λ<1)$,可得c=$\sqrt{λ+1-λ}$=1,可得焦点(±1,0).
由椭圆的定义可得:|AF1|+|AF2|=|BF1|+|BF2|=2a=2$\sqrt{λ+1}$.
∴△ABF1周长=4$\sqrt{λ+1}$.
(2)设直线AB的方程为:my=x-1,A(x1,y1),B(x2,y2).
联立$\left\{\begin{array}{l}{my=x-1}\\{\frac{{x}^{2}}{λ+1}+\frac{{y}^{2}}{λ}=1}\end{array}\right.$,化为:(λm2+λ+1)y2+2λmy-λ2=0,
△>0,y1+y2=$\frac{-2λm}{λ{m}^{2}+λ+1}$,y1y2=$\frac{-{λ}^{2}}{λ{m}^{2}+λ+1}$.
∴|y1-y2|=$\sqrt{({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}}$=$\frac{2λ\sqrt{λ{m}^{2}+λ+{m}^{2}+1}}{λ{m}^{2}+λ+1}$.
∴△ABF1面积S=$\frac{1}{2}×2c×$|y1-y2|=$\frac{2λ\sqrt{λ{m}^{2}+λ+{m}^{2}+1}}{λ{m}^{2}+λ+1}$=$\frac{2λ\sqrt{λ+1}}{\frac{1}{\sqrt{{m}^{2}+1}}+λ\sqrt{{m}^{2}+1}}$≤$\frac{2λ\sqrt{λ+1}}{2\sqrt{λ}}$=$\sqrt{{λ}^{2}+λ}$.当且仅当m=0时取等号.
∴△ABF1面积的最大值为$\sqrt{{λ}^{2}+λ}$.
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆的相交弦长问题、一元二次方程的根与系数的关系、三角形面积计算公式、基本不等式的性质,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | p∧(¬q) | C. | (¬p)∧q | D. | ¬p∨q |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{2\sqrt{3}}{3}$,$\frac{2\sqrt{3}}{3}$) | B. | (-∞,-1)∪(0,+∞) | C. | (-$\frac{2\sqrt{3}}{3}$,0) | D. | (-$\frac{2\sqrt{3}}{3}$,-1)∪({0,$\frac{2\sqrt{3}}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{12}$ | B. | $\frac{1}{2}$ | C. | $\frac{7}{12}$ | D. | $\frac{5}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 最大值是$\sqrt{2}$,周期是π | B. | 最小值是-2,周期是2π | ||
| C. | 最大值是$\sqrt{2}$,周期是2π | D. | 最小值是-2,周期是π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com