
| A. | 最大值是$\sqrt{2}$,周期是π | B. | 最小值是-2,周期是2π | ||
| C. | 最大值是$\sqrt{2}$,周期是2π | D. | 最小值是-2,周期是π |
分析 先利用两角和公式对函数解析式化简整理,进而根据正弦函数的性质求得函数的最小值和周期.
解答 解:f(x)=sinx+$\sqrt{3}$cosx=2($\frac{1}{2}$sinx+$\frac{\sqrt{3}}{2}$cosx)=2sin(x+$\frac{π}{3}$),
∵x∈R,
∴-1≤sin( x+$\frac{π}{3}$)≤1.
∴-2≤2sin( x+$\frac{π}{3}$)≤2.
则f(x)的最小值为-2.T=2π.
故选:B.
点评 本题主要考查了正弦函数的定义域和值域.解题的关键是对函数解析式的化简和角范围分析,以及对正弦函数的基础知识的熟练记忆,属基础题.


 优学名师名题系列答案
优学名师名题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
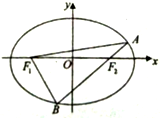 已知F1、F2是椭圆$\frac{x^2}{λ+1}+\frac{y^2}{λ}=1\;(0<λ<1)$在左、右焦点,直线AB经过F2交椭圆于A、B两点(A点在x轴上方),连结AF1、BF1.
已知F1、F2是椭圆$\frac{x^2}{λ+1}+\frac{y^2}{λ}=1\;(0<λ<1)$在左、右焦点,直线AB经过F2交椭圆于A、B两点(A点在x轴上方),连结AF1、BF1.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,-1] | B. | [2,3] | C. | [-2,2] | D. | [-1,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3 个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若x2-5x+6=0,则x=2”的逆否命题是“若x≠2,则x2-5x+6≠0” | |
| B. | 对命题p:?x∈R,使得x2+x+1<0,则?p:?x∈R,x2+x+1≥0 | |
| C. | 若x,y∈R,则“x=y”是“xy≥($\frac{x+y}{2}$)2中等号成立”的充要条件 | |
| D. | 已知命题p和q,若p∨q为假命题,则命题p与q中必一真一假 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com