
分析 如图所示,取BC的中点D,连接OD,AD,可得OD⊥BC,$\overrightarrow{AD}$=$\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC})$.又$\overrightarrow{AO}=\overrightarrow{DO}-\overrightarrow{DA}$,可得$\overrightarrow{AO}$•$\overrightarrow{BC}$=$(\overrightarrow{DO}-\overrightarrow{DA})$•$\overrightarrow{BC}$=$\overrightarrow{AD}•\overrightarrow{BC}$=$\frac{1}{2}({\overrightarrow{AC}}^{2}-{\overrightarrow{AB}}^{2})$=$(b-\frac{1}{2})^{2}$-$\frac{1}{4}$,再利用二次函数的单调性即可得出.
解答 解:如图所示,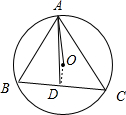
取BC的中点D,连接OD,AD.
则OD⊥BC,
$\overrightarrow{AD}$=$\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC})$.
∴$\overrightarrow{OD}•\overrightarrow{BC}$=0.
又$\overrightarrow{AO}=\overrightarrow{DO}-\overrightarrow{DA}$,
∴$\overrightarrow{AO}$•$\overrightarrow{BC}$=$(\overrightarrow{DO}-\overrightarrow{DA})$•$\overrightarrow{BC}$
=$\overrightarrow{AD}•\overrightarrow{BC}$
=$\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC})$•$(\overrightarrow{AC}-\overrightarrow{AB})$
=$\frac{1}{2}({\overrightarrow{AC}}^{2}-{\overrightarrow{AB}}^{2})$
=$\frac{1}{2}({b}^{2}-{c}^{2})$
=b2-b
=$(b-\frac{1}{2})^{2}$-$\frac{1}{4}$≥$\frac{1}{4}$,当且仅当b=$\frac{1}{2}$时取等号.
∴$\overrightarrow{AO}$•$\overrightarrow{BC}$的最小值为:$\frac{1}{4}$.
点评 本题考查了垂经定理、数量积运算性质、向量垂直与数量积的关系、二次函数的单调性,考查了推理能力与计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | { x|0≤x≤2} | B. | { x|1≤x≤2} | C. | {1,2 } | D. | Φ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,4] | B. | [2,4] | C. | [1,3] | D. | [2,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{81}$ | B. | -$\frac{1}{81}$ | C. | $\frac{1}{27}$ | D. | -$\frac{1}{27}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com