
【题目】已知函数 ![]()
(1)求函数f(x)的最小正周期和图象的对称轴方程.
(2)求函数f(x)的单调增区间.
(3)求函数y=f(x)在区间 ![]() 上的最小值,并求使y=f(x)取得最小值时的x的值.
上的最小值,并求使y=f(x)取得最小值时的x的值.
【答案】
(1)解:函数 ![]()
化简可得:f(x)= ![]() cos2x﹣sinxcosx﹣
cos2x﹣sinxcosx﹣ ![]()
= ![]() (
( ![]() cos2x)﹣
cos2x)﹣ ![]() sin2x﹣
sin2x﹣ ![]()
= ![]() cos2x﹣
cos2x﹣ ![]() sin2x﹣
sin2x﹣ ![]()
=cos(2x+ ![]() )-
)- ![]() ,
,
∴函数f(x)的最小正周期T= ![]() ,
,
由2x+ ![]() =kπ,(k∈Z),
=kπ,(k∈Z),
可得:x= ![]() ,(k∈Z),
,(k∈Z),
∴图象的对称轴方程为x= ![]() ,(k∈Z)
,(k∈Z)
(2)解:由 ![]() ,(k∈Z),
,(k∈Z),
可得 ![]()
∴增区间为 ![]()
(3)解:当x∈ ![]() 上时,
上时,
可得: ![]() ∈[
∈[ ![]() ,
, ![]() ],
],
当2x+ ![]() =π时,f(x)取得最小值为﹣1﹣
=π时,f(x)取得最小值为﹣1﹣ ![]() ;
;
此时解得x= ![]()
∴当 ![]() 时,最小值为
时,最小值为 ![]()
【解析】(1)利用二倍角以及辅助角公式基本公式将函数化为y=Acos(ωx+φ)的形式,再利用周期公式求函数的最小正周期,对称轴方程,(2)将内层函数看作整体,放到正弦函数的增区间上,解不等式得函数的单调递增区间;(2)x∈ ![]() 上时,求出内层函数的取值范围,结合三角函数的图象和性质,求出f(x)的最小值,即得到x)的取值.
上时,求出内层函数的取值范围,结合三角函数的图象和性质,求出f(x)的最小值,即得到x)的取值.
【考点精析】解答此题的关键在于理解正弦函数的单调性的相关知识,掌握正弦函数的单调性:在![]()
![]() 上是增函数;在
上是增函数;在![]()
![]() 上是减函数.
上是减函数.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex﹣e﹣x+4sin3x+1,x∈(﹣1,1),若f(1﹣a)+f(1﹣a2)>2成立,则实数a的取值范围是( )
A.(﹣2,1)
B.(0,1)
C.![]()
D.(﹣∞,﹣2)∪(1,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() cos4x+2sinxcosx﹣
cos4x+2sinxcosx﹣ ![]() sin4x.
sin4x.
(1)当x∈[0, ![]() ]时,求f(x)的最大值、最小值以及取得最值时的x值;
]时,求f(x)的最大值、最小值以及取得最值时的x值;
(2)设g(x)=3﹣2m+mcos(2x﹣ ![]() )(m>0),若对于任意x1∈[0,
)(m>0),若对于任意x1∈[0, ![]() ],都存在x2∈[0,
],都存在x2∈[0, ![]() ],使得f(x1)=g(x2)成立,求实数m的取值范围.
],使得f(x1)=g(x2)成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在[﹣1,1]上的奇函数,且f(1)=1,若m,n∈[﹣1,1],m+n≠0 时,有 ![]() .
.
(1)求证:f(x)在[﹣1,1]上为增函数;
(2)求不等式 ![]() 的解集;
的解集;
(3)若 ![]() 对所有
对所有 ![]() 恒成立,求实数t的取值范围.
恒成立,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方形ADEF与梯形ABCD所在的闰面互相垂直,AD⊥CD,AB∥CD,AB=AD=2,CD=4,M为CE的中点.
(1)求证:BM∥平面ADEF;
(2)求平面BEC与平面ADEF所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年年底,某商业集团根据相关评分标准,对所属20家商业连锁店进行了年度考核评估,并依据考核评估得分(最低分60分,最高分100分)将这些连锁店分别评定为A,B,C,D四个类型,其考核评估标准如下表:
评估得分 | [60,70) | [70,80) | [80,90) | [90,100] |
评分类型 | D | C | B | A |
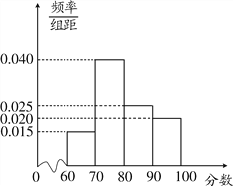 考核评估后,对各连锁店的评估分数进行统计分析,得其频率分布直方图如下:
考核评估后,对各连锁店的评估分数进行统计分析,得其频率分布直方图如下:
(Ⅰ)评分类型为A的商业连锁店有多少家;
(Ⅱ)现从评分类型为A,D的所有商业连锁店中随机抽取两家做分析,求这两家来自同一评分类型的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com