练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

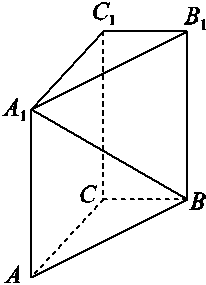
    如图，在直三棱柱ABC－A1B1C1中，∠ACB＝90°，AA1＝2，AC＝BC＝1，则异面直线A1B与AC所成角的余弦值是________．


    [解析]　由于AC∥A1C1，所以∠BA1C1(或其补角)就是所求异面直线所成的角．在△BA1C1中，A1B＝，A1C1＝1，BC1＝，cos ∠BA1C1＝＝.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    在空间直角坐标系中，A1是点A(-3,4,0)关于B(-1,2,3)的对称点，则|AA1|= （    ）

        A．          B．         C．9              D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    有5本不同的教科书，其中语文书2本，数学书2本，物理书1本．若将其并排摆放在书架的同一层上，则同一科目书都不相邻的放法种数是(　　)

    A．24  B．48  C．72  D．96

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某动点在平面直角坐标系第一象限的整点上运动(含x，y正半轴上的整点)，其运动规律为(m，n)→(m＋1，n＋1)或(m，n)→(m＋1，n－1)．若该动点从原点出发，经过6步运动到(6,2)点，则有________种不同的运动轨迹．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


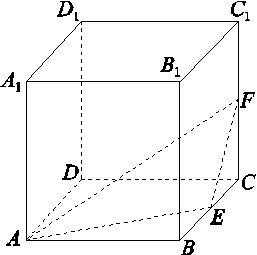
    如图，在棱长为1的正方体ABCD－A1B1C1D1中，点E，F分别是棱BC，CC1的中点，P是侧面BCC1B1内一点，若A1P∥平面AEF，则线段A1P长度的取值范围是(　　)

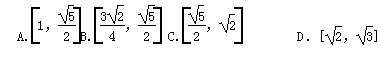
    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，底面为直角梯形的四棱柱ABCD－A1B1C1D1中，侧棱AA1⊥底面ABCD，E为A1B1的中点，且△ABE为等腰直角三角形，AB∥CD，AB⊥BC，AB＝2CD＝2BC.

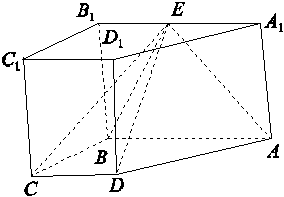
    (1)求证：AB⊥DE；

    (2)求直线EC与平面ABE所成角的正弦值；

    (3)线段EA上是否存在点F，使EC∥平面FBD？若存在，求出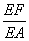；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知f(x)是定义在R上的偶函数，且对任意x∈R都有f(x＋4)＝f(x)＋f(2)，则f(2 014)等于(　　)

    A．0  B．3  C．4  D．6

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝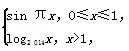

    若a，b，c互不相等，且f(a)＝f(b)＝f(c)，则a＋b＋c的取值范围是(　　)

    A．(1,2 014)                            B．(1,2 015) 

    C．(2,2 015)                            D．[2,2 015]

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    等比数列{an}中，a1＝2，a8＝4，函数f(x)＝x(x－a1)(x－a2)·…·(x－a8)，则f′(0)＝(　　)

    A．212  B．29  C．28  D．26

    查看答案和解析>>

    同步练习册答案