练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    等比数列{an}中，a1＝2，a8＝4，函数f(x)＝x(x－a1)(x－a2)·…·(x－a8)，则f′(0)＝(　　)

    A．212  B．29  C．28  D．26


    　A

    [解析]　f′(x)＝(x－a1)(x－a2)·…·(x－a8)＋x[(x－a1)(x－a2)·…·(x－a8)]′，

    ∴f′(0)＝(0－a1)(0－a2)·…·(0－a8)＝a1a2·…·a8＝(a1·a8)4＝84＝212.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    如图，在直三棱柱ABC－A1B1C1中，∠ACB＝90°，AA1＝2，AC＝BC＝1，则异面直线A1B与AC所成角的余弦值是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数y＝f(2x)＋x是偶函数，且f(2)＝1，则f(－2)＝(　　)

    A．2  B．3  C．4  D．5

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝|log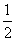x|，若m<n，有f(m)＝f(n)，则m＋3n的取值范围是(　　)

    A．[2，＋∞)                         B．(2，＋∞) 

    C．[4，＋∞)                            D．(4，＋∞)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    f(x)是定义在D上的函数，若存在区间[m，n]⊆D，使函数f(x)在[m，n]上的值域恰为[km，kn]，则称函数f(x)是k型函数．给出下列说法：

    ①f(x)＝3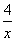－不可能是k型函数；

    ②若函数y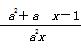＝(a≠0)是1型函数，则n－m的最大值为；

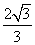    ③若函数y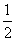＝－x2＋x是3型函数，则m＝－4，n＝0；

    ④设函数f(x)＝x3＋2x2＋x(x≤0)是k型函数，则k的最小值为.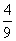

    其中正确的说法为________．(填入所有正确说法的序号)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数f(x)＝的零点个数为(　　)

    A．0  B．1  C．2  D．3

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知动圆C过定点M(0,2)，且在x轴上截得弦长为4.设该动圆圆心的轨迹为曲线C.

    (1)求曲线C的方程；

    (2)设点A为直线l：x－y－2＝0上任意一点，过A作曲线C的切线，切点分别为P，Q，求△APQ面积的最小值及此时点A的坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    甲、乙、丙三人参加某次招聘会，假设甲能被聘用的概率是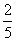，甲、丙两人同时不能被聘用的概率是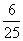，乙、丙两人同时能被聘用的概率是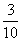，且三人各自能否被聘用相互独立．

    (1)求乙、丙两人各自能被聘用的概率；

    (2)设ξ表示甲、乙、丙三人中能被聘用的人数与不能被聘用的人数之差的绝对值，求ξ的分布列与均值(数学期望)．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设命题p：∃α0，β0∈R，cos(α0＋β0)＝cos α0＋cos β0；命题q：∀x，y∈R，且x≠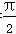＋kπ，y≠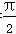＋kπ，k∈Z，若x＞y，则tan x＞tan y．则下列命题中真命题是(　　)

    A．p∧q                                 B．p∧(綈q)

    C．(綈p)∧q                             D．(綈p)∧(綈q)

    查看答案和解析>>

    同步练习册答案