
已知动圆C过定点M(0,2),且在x轴上截得弦长为4.设该动圆圆心的轨迹为曲线C.
(1)求曲线C的方程;
(2)设点A为直线l:x-y-2=0上任意一点,过A作曲线C的切线,切点分别为P,Q,求△APQ面积的最小值及此时点A的坐标.
解:(1)设动圆圆心坐标为C(x,y),根据题意,得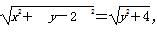
化简得x2=4y.
故曲线C的方程为x2=4y.
(2)设直线PQ的方程为y=kx+b,
由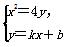 消去y,得x2-4kx-4b=0.
消去y,得x2-4kx-4b=0.
设P(x1,y1),Q(x2,y2),
则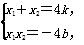 且Δ=16k2+16b.
且Δ=16k2+16b.
以点P为切点的切线的斜率为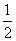 x1,其切线方程为y-y1=
x1,其切线方程为y-y1=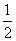 x1(x-x1),
x1(x-x1),
即y=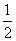 x1x-
x1x-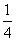 x
x ,
,
同理过点Q的切线的方程为y=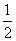 x2x-
x2x-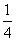 x
x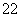 .
.
设两条切线的交点A(xA,yA),
∵x1≠x2,解得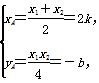
即A(2k,-b),
则2k+b-2=0,即b=2-2k,代入Δ=16k2+16b=16k2+32-32k=16(k-1)2+16>0,
∴|PQ|=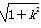 |x1-x2|
|x1-x2|
=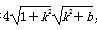
又A(2k,-b)到直线PQ的距离为d=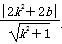 ,
,
∴S△APQ=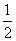 |PQ|·d=4|k2+b|·
|PQ|·d=4|k2+b|· =4(k2+b)
=4(k2+b) 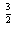 =4(k2-2k+2)
=4(k2-2k+2) 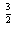 =4[(k-1)2+1]
=4[(k-1)2+1] 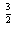 ,
,
∴当k=1时,S△APQ最小,其最小值为4,此时点A的坐标为(2,0).


科目:高中数学 来源: 题型:
已知函数f(x)=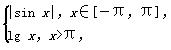
x1,x2,x3,x4,x5是方程f(x)=m的五个不等的实数根,则x1+x2+x3+x4+x5的取值范围是( )
A.(0,π) B.(-π,π)
C.(lg π,1) D.(π,10)
查看答案和解析>>
科目:高中数学 来源: 题型:
等比数列{an}中,a1=2,a8=4,函数f(x)=x(x-a1)(x-a2)·…·(x-a8),则f′(0)=( )
A.212 B.29 C.28 D.26
查看答案和解析>>
科目:高中数学 来源: 题型:
某一部件由三个电子元件按下图方式连接而成,元件1或元件2正常工作,且元件3正常工作,则部件正常工作,设三个电子元件的使用寿命(单位:小时)均服从正态分布N(1 000,502),且各个元件能否正常工作相互独立,那么该部件的使用寿命超过1 000小时的概率为( )
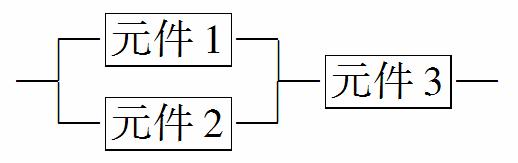
A.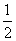 B.
B.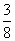 C.
C.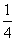 D.
D.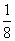
查看答案和解析>>
科目:高中数学 来源: 题型:
体育课的排球发球项目考试的规则是:每位学生最多可发球3次,一旦发球成功,则停止发球,否则一直发到3次为止.设学生一次发球成功的概率为p(p≠0),发球次数为X,若X的数学期望E(X)>1.75,则p的取值范围是( )
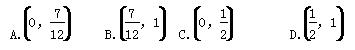
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=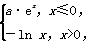
其中e为自然对数的底数,若关于x的方程f(f(x))=0有且只有一个实数解,则实数a的取值范围为( )
A.(-∞,0) B.(-∞,0)∪(0,1)
C.(0,1) D.(0,1)∪(1,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
已知命题p:“∀x∈[1,2], x2-ln x-a≥0”与命题q:“∃x∈R,x2+2ax-8-6a=0”都是真命题,则实数a的取值范围是________.
x2-ln x-a≥0”与命题q:“∃x∈R,x2+2ax-8-6a=0”都是真命题,则实数a的取值范围是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com